What is the upper bound of total number of divisors of divisors of a number ?
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 159 |
| 5 | atcoder_official | 156 |
| 6 | djm03178 | 153 |
| 6 | adamant | 153 |
| 8 | luogu_official | 149 |
| 9 | awoo | 148 |
| 10 | TheScrasse | 146 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2025 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 17.02.2025 07:06:41 (j1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










If a is divisor of x and y and both x and y are divisors of z, do you count a twice?
yes
then you may consider the upper bound to be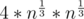 , as the upper bound on number of divisors is
, as the upper bound on number of divisors is  (verified upto n = 1018)
(verified upto n = 1018)
But where does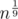 come from? Do you assume that divisors of n are of magnitude
come from? Do you assume that divisors of n are of magnitude  ? That isn't true.
? That isn't true.
I don't know if I was high writing that... My bad :(
Let f(n) be the number of divisors of divisors of n. If we are going to use a bound for d(n), we may use the identity:
where rad(n) and ω(n) are the product and the number of distinct prime divisors of n, respectively. That formula can be obtained by noting that f is multiplicative (being the Dirichlet convolution of d and 1, or the triple Dirichlet convolution of 1), and multiplying everything after getting .
.
Now, using the simple estimate
(which comes from the fact that
and increasing each term by 1 multiplies each bracket by at most 3/2)
we get
According to the last column of this table, talking only "competitive programming numbers" into account: this bound is better than the trivial
bound by ~ an order of magnitude, but should also not be very far from the truth - the worst cases have several prime factors, with only the exponent on the prime number $2$ being significant.
Of course, the asymptotic behaviour of d(n) has already been well-explained here, and even better on What's New. I couldn't obtain a real-world bound using this kind of approach, though.
Also,
Unable to parse markup [type=CF_TEX]
is buggy here. I think there is a problem with parsing the comments.if your purpose is not mathematical , you can approximately find by using brute force (I mean , you don't have a time limit in your computer)