I'm trying to come up with a recursive solution for this problem but I haven't been able to so far. Any advice/pointers here?
I tried 0-1 knapsack style but there is an issue with backtracking the array.
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 161 |
| 4 | Um_nik | 159 |
| 4 | atcoder_official | 159 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 150 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Jan/31/2025 12:59:50 (i1).
Desktop version, switch to mobile version.
Supported by
It appears that the statement is actually asking for the number of permutations of 1... n with k inversions. If In(t) is the number of permutations of size n with t inversions, then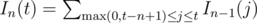
. This recurrence can be calculated in O(nt) using prefix sums on In.