Enchom's blog

Invitation to CodeChef July Long Challenge 2018!
By Enchom, history, 6 years ago, In English

Hello CodeForces Community!

We’re excited to invite you for the July Long Challenge 2018 sponsored by ShareChat. Join us for ten intense days of coding challenges! Joining me on the problem setting panel are:

And special thanks to mgch (Misha Chorniy) for coordinating the contest preparation!

I hope you will enjoy solving them. Please give your feedback on the problem set in the comments below, after the contest.

Contest Details:

Time: 6th July 2018 (1500 hrs) to 16th July 2018 (1500 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.

Contest link: https://www.codechef.com/JULY18

Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.

Prizes: Top 10 performers in Global and Indian category will get CodeChef laddus, with which the winners can claim cool CodeChef goodies. Know more here: discuss.codechef.com/questions/51999/how-do-i-win-a-codechef-goodie.
(For those who have not yet got their previous winning, please send an email to [email protected])

Good Luck!
Hope to see you participating!!

  • Vote: I like it
  • +73
  • Vote: I do not like it

Comments Comments (26)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve NMNMX ? Editorial link is broken.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    For each element of the array, count how many times it is written down.

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    Sort the array A[] = {a1, a2, ..., an}

    , we need to compute aixi

    xi is the number of subsequences in which ai is included but not as the Min. nor the Max.

    let's compute y instead, where y is the number of subsequences where ai is the Min. or the Max.

    which is choosing all other k - 1 numbers from left or right respectively.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    brute force for every possible pair of number such that pair(a,b) is smallest and largest numbers in the sequence of length k and use the combnatorial formula as MeshOmarYasser mentioned. You can calculate nCr by precomputing binomial table by recurrence nCr = (n-1Cr-1+ n-1Cr)% (p-1) where p is 1e9+7

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Why do you MOD with p-1 and not p?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Because of fermat little theorem ap - 1 ≡ 1modp.

        which gives ax ≡ ax%(p - 1)modp

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          How did you get from the first step to the second?

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it +2 Vote: I do not like it

            Let's say you want to compute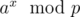 where x > p . Now by division algorithm x = q * (p - 1) + r

            By Fermat's little theorem it reduces to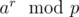 , where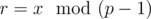

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              6 years ago, # ^ |
                Vote: I like it 0 Vote: I do not like it

              This is fantastic! Thanks! I was really looking for this result during the contest.

              → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

How to solve Sub task 3 for PDELIV . I tried modifying Li Chao segment tree by keeping note of the nodes modified by insertion of each parabola. But laster found out that each parabola can affect more than log N nodes of the segment tree hence would not pass TL.

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 3   Vote: I like it +7 Vote: I do not like it

    Sort pizzerias by position, and construct a segment tree of CHT (each node [L, R] contains a CHT of lines between L and R).

    To get the answer for a consumer, you don't need to remove a line from your structure.

    Now, supose there are 11 pizzerias, and consumer i doesn't like 3, 7 and 9. To answer this, you should get the minimum of 4 queries: [1, 2], [4, 6], [8, 8] and [10,11]. This works because the sum of forbidden pizzerias is at most 4 * 10^5 and the number of queries is about (N + M). The complexity of the query is log(N)^2 (one log from segment tree and one from CHT).

    → Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

How to solve Reach Eq

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    The problem in simpler terms is the probability of forming an n-gon with n non-negative real side lengths such that their sum is constant(k).

    Note: In order to form a polygon, the all side lengths must be less than k/2.

    Ans: 1 — n/(2^(n-1))

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      formula 1-n/2^(n-1).

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        The probability will be independent of k.

        Did you get an AC with the above formula?

        → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to get 100 points on PFRUIT? I got 50 points with moment-generating functions and FFT, but reached this bottleneck:

Evaluate 1p + 2p + ... + xp for all p between 1 and k and for 2n different values of x (where n·k ≤ 105).

Is it possible to do this fast enough? Or is there a completely different way of solving the problem?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Can you provide an explanation for your 50 point solution?

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Consider the multinomial theorem. Try writing (A1+A2+...+An)^k as product of n polynomials.

    This can be written as product of e^(Aix). The coefficient of x^k is what we are looking for. To handle A,B,C.. a little thinking gives us that answer is simply coefficient of x^k in product of ( sum of e^ix where i goes from Ai to Bi ).

    The sum is a GP sum..the rest is just log,exp,inverse of polynomials.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      I understand that it is .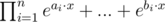

      We can obviously convert this to product of many geometric series. But the inverse of 1 - ex does not exist, as the constant term is 0. How can we use FFT over this equation to open the products ? I was stuck on this for much time.

      BTW, it is possible to get array A[] of size k, where A[i] is sum of ith powers of first n numbers in k·log2(k) time.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it +6 Vote: I do not like it

        "" But the inverse of 1 - e^x does not exist ""

        yes you are right. I encountered this situation as well.

        However this is very easy to overcome.

        Notice that the complete term is e^(Ax)*(e^(Lx)-1)/(e^x-1) where L = B-A+1

        both e^(Lx)-1 and e^x-1 do not have a constant term. so you can simply cancel out one power of 'x' from both of them and then both will have a constant term.

        now inverse of e^x-1 does exist.

        → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You can use lagrange interpolation for computing it in O(N * K^2). Consider the function f(n, p) = 1^p + 2^p + ... + n^p. It can be proved that f(n, p) is a p + 1 degree polynomial in n. For example, 1 + 2 + .. + n = n(n + 1) / 2, 1^2 + 2^2 + ... + n^2 = n(n + 1)(2 * n + 1) / 6. Now for each p, you can interpolate this polynomial using only O(p + 1) values. And you can compute this value for n values in O(n * p). But still it won't solve your problem for large k.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve SUBWAY?

→ Reply