Hello Codeforces,
Recently I came across a problem where we have to output the minimum number of fibonacci terms needed to make up a number. Repeating the terms to make up the representation is allowed. The fibonacci sequence 1,2,3,5,8,13,21.. will be used for all cases.
I can explain better with an example, lets say N=6, then the answer is 2, you can use the numbers 1 and 5 to make 6, another combination is 3 3, which also gives the optimal answer 2. However in this question we only need the minimum number of terms, not what those terms are.
Other examples: input = 5 output = 1 input = 7 output = 2 input = 19 output = 3
I tried out some examples and even submitted the greedy algorithm on this problem, which is to keep subtracting the largest fibonacci number possible which still keeps the result non-negative, and adding 1 for each of those terms subtracted. A few blogs on the same topic give this algorithm for solving the problem, however no proof on correctness.
A quick wikipedia search yielded Zuckendorf theorem, which just proves uniqueness with non-adjacent terms, I was unable to extend it to greedy or minimum.
Does anyone have a proof on correctness(or a counter-case is welcome too :D ) ?
Thank You Codeforces!











[ DELETED ]
Correct answer is 89+21 = 110. Greedy works just fine.
First of all, let's prove that with the first n fibonacci numbers, you can get all numbers in interval [0, fib(n) + fib(n - 1)], we can do that by induction:
Now it should be easier to prove the greedy algorithm: as we are interested in the minimum number of fibonacci terms to use,there are no reasons not to take the biggest one that fits the interval as we'll be always able to get any possible sum anyway. And for the case that dush1729 mentioned, just allow the possibility of repeated numbers and your greedy algorithm will work.
If I understand you correctly, your statement is "If we can get any number in interval [0, x] using some sequence, then optimal way to present some number in [0, x] is to take the maximum number from sequnce". But that's not true.
Let's look at this sequence: 1 1 2 4 5 6 10 ... . It's easy to prove that we can get any number from 1 to 10. Greedy will get 9 = 6 + 2 + 1. But the correct answer is 9 = 5 + 4.
So your proof is not enough, you just prooved that every number can be present using only fibonacci numbers, but not the correctness of greedy algorithm.
You are right, thanks. My last statement doesn't make much sense either :)
If you are interested in formal prove:
Let fi be the maximum fibonacci number that repeated k > 1 times in optimal number's presentation.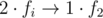 , and your presentation became shorter, so it's not optimal. Therefore i > 1
, and your presentation became shorter, so it's not optimal. Therefore i > 1
If fi = 1, then you may change
If k ≥ 3, let's make some changes: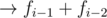
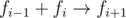
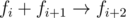
fi (only one!)
this means 3·fi = fi - 2 + fi + 2
Presenation became shorter by at least one number, hence it's not optimal.
If k = 2,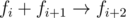 therefore it's not optimal. Otherwise:
therefore it's not optimal. Otherwise:
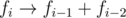
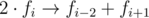
If there is fi + 1 in your presentation, then you can change
fi + fi - 1 = fi + 1
this means
As we proved before, fi + 1 now repeated only one time in your presentation. Therefore, your presentation didn't become shorter, but the largest number that now can be repeated twice became smaller. So, using math induction, you can continue that process. On each step, largest number repeated twice will be reducing, and this process finite, so at the end you will get optimal presentation there each number repeated only once.
P.S. There can be only one presentation without repeating numbers therefore it's optimal.
Thank you so so much, I had been breaking my head over it for the entire morning. How do you come up with such proofs, is there an article that can teach me to do that ?
Here is another look at the proof, which visualizes the problem via Fibonacci numeral system, and then uses its properties.
Introduce the Fibonacci numeral system. That is, the digits are multiplied by 1, 2, 3, 5, 8, 13, 21, ... For example, 25 = 21 + 3 + 1, so it can be expressed as 1000101. As in your solution, to obtain 1000101, we greedily select the largest Fibonacci number, subtract it and add 1 to the respective digit.
In the Fibonacci numeral system, there can't be two consecutive 1s. Suppose we had consecutive 1s. Look at the highest such pair. They correspond to some Fk and Fk + 1, which sum to Fk + 2. But our greedy algorithm would have added 1 to the digit number Fk + 2 instead, so this couldn't have happened. For the same reason, we won't get digits greater than 1 at all.
If we can't have two consecutive 1s, we can't express a higher digit by lower ones. Indeed, we can prove by induction that 1 + (F1 + F3 + F5 + F7 + ... + F2k - 1) = F2k. For example, 1 + (1 + 3 + 8 + 21) = 34. The same goes for even indices: 1 + (F2 + F4 + F6 + ... + F2k) = F2k + 1. For example, 1 + (2 + 5 + 13 + 34) = 55.
So, in Fibonacci numeral system, we actually have the same property as in decimal: when we have a number like 1000...00 with n zeroes, it is greater than any d1d2...dn with n digits.
We now see that, when we can pick the greatest possible Fibonacci number, we should pick it. Otherwise, we either won't get the required a sum with lower Fibonacci numbers, or will have to pick two consecutive Fibonacci numbers, some Fk and Fk + 1, which is non-optimal since we could have picked one Fibonacci number Fk + 2 instead of these two.
You should add to such proof the fact that "repeating numbers is not useful" (you start by assuming only 0 and 1 in the numeral system), I am assuming that is what's stopping the OP from being happy with the Wikipedia proof.
To address that, I've added a phrase at the end of point 2. But you are right, it's obscure, mostly because I didn't want to elaborate.
Essentially, as 2Fk ≥ Fk + 1, the highest digit which is 2 or greater could not have appeared if we followed the greedy algorithm, because another Fk + 1 would appear instead.
What I mean is that a proof of "there is no better solution than the one given by writing the number in Fibonacci base using only 0 and 1" is missing, not that the greedy algorithm itself would produce a "2", which is impossible because of what you say.
That is, in principle something like "002002" might be a better solution (uses less terms in total) than writing something like "101010101" (if they represented the same number). Such a thing would mean, algorithmically, that it would be best to "hold on" and not pick a certain term, in order to pick "two" of a smaller term that will appear later. That can't happen of course because the greedy algorithm is indeed correct, but it requires some proof.
The proof for that is given for example by Ralsei, or by the very similar argument in my comment, which only address this part about "repeating terms".
I agree 2Fk>=Fk+1, and that is the greedy algorithm produces Fk+1. But what if there is an optimal solution which involves repeating Fk-1 3 times, because we can find a very short representation for N-(Fk-1) from there on.
Well of course I cant give an example for such a case, because greedy is correct, but it is not addressed in your proof.
More concretely, lets say A<B<N. And Fk be the largest fibonacci number less than N. Also, N-Fk = B, and N-2*(Fk-2) = A.
If we didn't assume the correctness of greedy beforehand, one could think that, representation of A is in 3 terms, but B takes 14 terms. So what do you do about cases where ; not adjacent ; but the same fibonacci numbers repeat. As elsantodel90 says, there is nothing stopping the indices for fibonacci numbers from exceeding one in someone else's representation.
Sorry if I didn't understand your proof completely :(
Hmm, that's indeed missing, sorry! Here is a take at the missing piece.
If we have digits at least 2, consider any such digit. We can then change 2Fk into Fk - 2 + Fk + 1. This is because 2Fk = (Fk - 2 + Fk - 1) + Fk = Fk - 2 + (Fk - 1 + Fk) = Fk - 2 + Fk + 1. So, we decreased a digit which was at least 2, and the total sum of digits remained the same.
Note that the sum of digits from the bottom and up to this position also decreased. So, for any position, this transformation can happen only a finite number of times, which proves that there will eventually be no more causes for transformation.
Gassa this is such an awesome proof...
There was a task based on this fact on POI The Task . You can find an editorial in Polish with a really good explanation and proofs.
An optimal solution never uses two consecutive Fibonaccis (could be replaced by the next).
No need to use the same number twice is the other key:
Suppose your optimal solution uses the Fibonacci number following a1 and a2 twice. So your Fibonacci sequence has the following four numbers somewhere:
a1, a2, a1 + a2, a1 + 2a2
And we suppose that a1 + a2 is used twice. You could use a1 and a1 + 2a2 instead, because a1 + (a1 + 2a2) = 2(a1 + a2), to avoid repeating a1 + a2.
When this technique is applied to the largest repeated Fibonacci in your solution, you get another optimal solution with a smaller largest repeated Fibonacci (notice that a1 + 2a2 does not get repeated, because it could not be in your original solution or it would have two consecutive Fibonaccis), so you can iterate this process and clean your solution of repetitions.
Special cases: terms 1 and 2 do not have two preceding terms, and one cannot apply the previous argument. But using two ones is never optimal (1+1=2), and using 2+2=1+3, one can also eliminate duplicated twos, leaving only possibly repeated ones.
Knowing that the solution has no repetitions and never uses two consecutive Fibonaccis, uniqueness of such a solution is proved as you say you already found, and the greedy algorithm just computes such a solution.
Could you explain these two lines :
what do you mean ?
I fixed the formatting of my post, it might be much more readable now.