https://szkopul.edu.pl/problemset/problem/l85hlaT4lDfPzwm3IPUHIMVo/site/?key=statement
I'm getting stuck at this problem. Could you give me a hint ? Thanks.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
https://szkopul.edu.pl/problemset/problem/l85hlaT4lDfPzwm3IPUHIMVo/site/?key=statement
I'm getting stuck at this problem. Could you give me a hint ? Thanks.
| Name |
|---|



Auto comment: topic has been updated by EternalFire (previous revision, new revision, compare).
Well, I am not able to think of any solution and looks like no one helped you so here is the code by ko_osaga if you didn't come across it yet.
Thank you.
Notice that for any 3 length AP , the first and last term must be of the same parity , hence if we can we can ensure that for every middle element , all elements with odd parity lie on left and all with even parity lie on right , we are done.
so just pick the middle element of 1..n , put all odd terms on left and all even terms on right , and recursively solve them.
But then won't all elements on depth two of the recursion be of the same parity? Can you explain the solution in a with some more details.
Let's look at the bits of each number. In depth K of the recursion we'll look at the Kth least significant bit.
In depth 0 we put all numbers with the first bit 0 at the left part, and the remaining on the right. Any arithmetic progression cannot contain 2 elements from both halves, so we recursively solve for the left part and right part, and now look at the second bit, and so on.
For each layer of recursion we do time and there are
time and there are 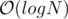 layers.
layers.
I also thought that looking at second bit, third bit and so on, depending on layer will work, but I don't think it is correct.
It shouldn't work, because we want the equation a0 + 2 * d ≠ a2 to hold, which only forces the 0-th bit to be distinct.
On some layer K, we know that for all elements there, all the bits before the Kth one are equal, which forces the difference of an AP there to have all bits before the Kth be 0, which means all previous bits have no effect on the Kth one so this is exactly a subproblem.
okay , so for simplicity we assume N = 2m - 1 or N = 2m , if not we can always find the smallest such number ≥ N and remove the larger elements before printing.
lets say N = 15 , then middle element = 8 , all elements on left are 7, 9, 5, 11, 3, 13, 1, 15 , the ones on right are 8, 6, 10, 4, 12, 2, 14 its clear that the difference between consecutive elements is 2 so we can instead treat them by reducing to 1..N / 2.
This reduced the problem from 15 to 7 and 8 , 7 can be solved similarly , for 8 , we again pick 5 as middle element , push 1, 3, 5, 7 on left and 2, 4, 6, 8 on right and solve again. [ We basically just need to maintain that after splitting , differences is 2]
actually the 2n - 1 case is useless and we can go straight to the next power of 2 and get the usual ordering we do before FFT.