Let's discuss problems.
What was your solution for problems E and J?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 154 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Let's discuss problems.
What was your solution for problems E and J?
| Name |
|---|



Auto comment: topic has been translated by SimB4 (original revision, translated revision, compare)
We've done problem G with Suffix Array + Segment Tree + Treap in each vertex of ST. May be there is simpler approach?
More details?
Let's reverse both strings. Then let build suffix array on string S'#T'. For each suffix you have pair (suffixIndex, a[suffixIndex]). Now, to find answer to query you need to find appropriate suffix of t in suffix array, then find interval where this t can be found as prefix using lcp. On this interval you need to find sum of a[i]'s where i is in [s1, s2], which can be done with Segment Tree + Treap in each node of Segment Tree.
What is the upper bound we need to count knapsack dp in D? I counted up to 500000 and got OK, but how to prove it?
It is guaranteed that aj = 1 for some j (1 ≤ j ≤ n). The answer <= 4000 => upper bound is 400000
Actually you can use upper bound = 4000 as you can move both up and down, so you can calculate answer in such a way that all middle values do not exceed max(k, 2·max(ai)).
J is an old GCJ problem.
(I had trouble with TL, maybe because of a heavy constant — if someone has a solution that works under 0.5s, could you share it?)
K: Let dp[x] be the optimal score we can get from a square of side lengths x. It turns out that dp[x] is approximately 0.0755605242906x3, so with some calculus we can get the optimal square size approximately. Is there a simpler solution?
We can find dp[x] with binary search
For a given x, we want to find i that maximizes (x - 2i)2i + dp[i] * 4. How do we use binary search here?
Where V is:
So, did you assume that the function is convex?
Actually the function is not convex (for example, print V for a = b = 10000 and various x, the function has both local maximum and local minimum), but it seems your solution works for magical reasons.
For random a = b = N I found only one local maximum and only one local minimum; for example, if N = 10000, then local minimim is at 1736 and local maximum at 4462,and if N = 3456, then local minimim is at 600 and local maximum at 1542. Each time the local minimum is greater than N / 4, so it doesn't infuence on the binary search.
We assumed that since derivative is linear then optimal solution can be found incrementally (optimal point for dp[x] shouldn't be less than optimal point for dp[x + 1]) or with ternary search.
We can calculate dp[x] linearly.
Lets define z as optimal size of the squares that we need to cut from corners of our square of size x to get optimal result dp[x].
We can notice that z can only increase if we increase x. So when we calculate dp[x] we can keep this value z that is currently provides best score for x - 1, we can push z to the right while it improves our answer. So z will be pushed right less than 106 times.
J code is here. This runs in 215 ms.
How to solve E?
We have quite complicated solution, I wander if there exists a simpler one.
Find all blocks of the graph. If there exists block with vertices of all three colors then answer is YES. You can always find necessary cycle. For example, it's possible to find an edge with two endpoints of distinct colors, find a vertex with the third color and find a cycle containing that edge and that vertex (as I remember there is a theorem that a graph is 2-vertex-connected if and only if for each edge and vertex of the graph there exists simple cycle going through the edge and the vertex).
Cycle can be found with maxflow if the vertex is source and endpoints of the edge are sink. Complexity will be O(maxflow·(M + N)) = O(2(M + N)) = O(M + N).
If no such block exists answer is NO.
If a tour exists, it will be contained in a single block (biconnected component). Hence we process each block separately. If every block contains at most two types of breweries, the answer is NO.
Otherwise take vertices a, b, c of different types of breweries and compute two internally vertex disjoint paths between every pair of them. If they contain the third type of brewery, we join the two paths to a cycle to get a tour.
Otherwise (this part actually never executed on the judge) just remember one path between every pair. Our goal is to make these 3 paths internally vertex-disjoint. If we take two paths, then they share one vertex X out of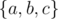 and the other two endpoints Y, Z differ. Let U be the vertex furthest from X that is contained in both of the paths. Note that U has the same brewery type as X. Taking the subpaths from Y to U and form Z to U makes them vertex disjoint without loosing any brewery type. Repeat this for all pairs.
and the other two endpoints Y, Z differ. Let U be the vertex furthest from X that is contained in both of the paths. Note that U has the same brewery type as X. Taking the subpaths from Y to U and form Z to U makes them vertex disjoint without loosing any brewery type. Repeat this for all pairs.
Is there a nice Solution for I? If you do binary search for the water level and decompose the iceberg into tetrahedra with 3D-convex-hull, the problem reduces to finding the volume of a tetrahedron clipped with a half-space.
My approach was to integrate the horizontal cross-section (it's piecewise quadratic if we exclude discontinuities) of the tetrahedron by using Simpson's rule on each piece. This leads to some problems with faces perpendicular to ez, as the cross-section is not continuous there.
You can clip not tetrahedra, but facets of the iceberg (it is much easier), then you have to compute the volume of a convex polyhedron defined by its facets, which is straightforward.
But how do you find faces easily? Won't n^4 timeout? or it's not if you check the points in random order?
I found faces in O(n^4) and it passed even though I did all calculations in long doubles.
That's my approach as well (integrate piecewise quadratic function). To avoid the issues you mention, I just used segments [i;i+1] (since z is between -100 and 100) and integrated using three points i+0.25, i+0.5, i+0.75, to avoid hitting any vertices. And to find the cross-section I just intersected segments collecting all pairs of points with the plane and found convex hull. That seems to make the code quite sane, modulo convex hull with floating-point inputs.
It seems I am missing something simple in B, probably because I overcomplicate the problem :).
I've reduced the problem to counting the number of of topological orderings in a graph of a special form (which look somewhat like a Young tableaux, but 'right-aligned' instead of the usual 'left-aligned').
What am I missing?
Bruteforce precalc works.
3 1
4 1
5 2
6 5
7 33
8 319
9 9666
10 484101
11 86126251
12 921102616
13 690667755
14 277772735
15 168927647
16 863966777
17 656710249
18 529211723
19 952552517
20 226276192
21 197949884
22 305182080
23 473057943
24 9119576
25 607610013
26 800401364
27 125881901
28 404394074
29 47341655
30 126866039
31 937077929
32 680342212
Yet another representation: if we think of target string as concatenation of strings A = "01", then operations mean that we can push each A to left for 1 position (first push is creation). we can see that every state of process can be described as point (l1, l2, l3, ..., lk), k — number of A's, and li — number of pushes of Ai to left and li > li + 1 must be satisfied for every i. Hence, the whole process is a path from (0, 0, ...0) to (n - 1, n - 3, ..., 2 - n%2). So You are to calculate the number of specific paths. Actually, the reason that first answers are Catalan numbers (1, 1, 2, 5) is that it counts the number of paths not exceeding diagonal.