Блог пользователя DimmyT

Почему у меня Тл?
Автор DimmyT, история, 7 лет назад, По-русски

на задаче 977F - Последовательная подпоследовательность у меня Тл решение с unordered_map 37945413 но точно такое же решение с map 37989920 у меня прошло. Это случаем не баг, ведь unordered_map работает быстрее map . Или я ошибаюсь?

UPD:

Нашел крутые материалы про unordered_map:

https://codeforces.me/blog/entry/62393

https://codeforces.me/blog/entry/21853

  • Проголосовать: нравится
  • +22
  • Проголосовать: не нравится

»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Интересно. Действительно, отличие только в замене unordered_map<int, pair<int, int>> на map<int, pair<int, int>>. Однако если добавить к ключам случайный шум (например, a[i] ^ 23901755 вместо a[i]), то проходит: 37990845. Работает не всегда, если шум меняет только младшие биты, то не помогает: 37990781 (TL на одном из следующих тестов).

Кажется, что в этой конкретной версии GCC очень плохой хэш для ключей int и случаются тонны коллизий, из-за чего решение начинает вместо 0.3 секунд работать >2 секунд. Ну или кто-то заморочился и подобрал специальный тест с коллизиями против конкретной версии (сомневаюсь, так как там вроде генератор довольно простой).

У меня локально с версией 7.3.0 не воспроизводится. Если перепослать на CF под более новым GCC, то снова воспроизводится: 37990911 и 37990919.

→ Ответить
»
7 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

greencis, а с какой идеей был сделан взлом — просто большой тест или антихэш?

→ Ответить
  • »
    »
    7 лет назад, # ^ |
    ← Rev. 5   Проголосовать: нравится +12 Проголосовать: не нравится

    Антихэш. Я стараюсь сделать так, чтобы все ключи попали в как можно меньшее число бакетов, чтобы доступ к элементам длился максимально долго. В компиляторах GCC хэш от числа -- это само число, а номер бакета определяется как (key % bucket_count). Зная количество бакетов на максимальном тесте, легко подобрать соответствующие числа.

    В C++11 и C++14 расширение хэш-таблицы происходит немного по-другому, нежели в C++17: видимо, константа отличается. А решения на MS C++ я ломать пока не умею: там целые числа хэшируются при помощи специальной функции из нескольких арифметических операций, которую не так просто обратить уже умею, обращение совсем простое.

    → Ответить
    • »
      »
      »
      7 лет назад, # ^ |
        Проголосовать: нравится 0 Проголосовать: не нравится

      А не подкинете функцию? Что-то я за 2 минуты не нашёл. Мне казалось, что её было довольно легко сломать тоже.

      → Ответить
      • »
        »
        »
        »
        7 лет назад, # ^ |
        ← Rev. 2   Проголосовать: нравится +10 Проголосовать: не нравится

        Конечно. В файле VC\include\xhash можно найти следующий код:

        size_t operator()(const _Kty& _Keyval) const
	{	// hash _Keyval to size_t value by pseudorandomizing transform
	long _Quot = (long)(hash_value(_Keyval) & LONG_MAX);
	ldiv_t _Qrem = _CSTD ldiv(_Quot, 127773);

	_Qrem.rem = 16807 * _Qrem.rem - 2836 * _Qrem.quot;
	if (_Qrem.rem < 0)
		_Qrem.rem += LONG_MAX;
	return ((size_t)_Qrem.rem);
	}

        Любопытный факт, кстати: 127773·16807 + 2836 = 231 - 1.

        UPD: попытка загуглить число 16807 выдаёт ссылку на статью про ГСЧ Лемера.

        → Ответить
        • »
          »
          »
          »
          »
          7 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится

          1) Насколько я помню кол-во бакетов степень двойки, то есть мы по факту хотим чтобы младшие несколько битов совпадали. Поэтому можно от хеша брать только последние биты. Тестил таким кодом (16 для примера):

          >>> def f(x):
...   q = x // 127773
...   r = x % 127773
...   z = 16807 * r - 2836 * q
...   return z % (2 ** 16)

          Пусть мы знаем y f(y) = 0, тогда f(y + 1) = 16807 (почти всегда)

          >>> for i in range(20 << 16):
...   if f(i) == 0:
...     print(i, f(i + 1))
...
0 16807
65536 16807
174569 16807
240105 16807
283602 16807
349138 16807
392635 16807
458171 16807
567204 16807
632740 16807
676237 16807
741773 16807
785270 16807
850806 16807
959839 16807
1068872 16807
1134408 16807
1177905 16807
1243441 16807
1286938 16807

          Аналогично f(y + 2) == 2 * 16807 почти всегда.

          Остается перебрать(или предпосчитать) нулевые хеши.

          → Ответить
      • »
        »
        »
        »
        7 лет назад, # ^ |
        ← Rev. 2   Проголосовать: нравится +10 Проголосовать: не нравится

        А, так это же просто умножение ключа на число 16807 по модулю 231 - 1 без long long. Получается, для обращения хэш-функции достаточно домножить значение на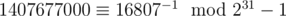 , и мы получим те числа, которые нам нужны.

        → Ответить
        • »
          »
          »
          »
          »
          7 лет назад, # ^ |
            Проголосовать: нравится 0 Проголосовать: не нравится

          Да, видимо, так гораздо проще, чем то, что я написал :)

          → Ответить
»
5 лет назад, # |
← Rev. 2   Проголосовать: нравится -35 Проголосовать: не нравится

Why so much dislikes?

→ Ответить
»
5 лет назад, # |
  Проголосовать: нравится +4 Проголосовать: не нравится

Good amount of discussion on this same topic can be found here. Read all comments.

→ Ответить
»
5 лет назад, # |
  Проголосовать: нравится +1 Проголосовать: не нравится

The worst case time complexity of operation in unordered_map is O(n) rather than the expected O(1),moreover the complexity of unordered_map is amortised O(1) ,whereas for map is O(log n). Similar thing had happened to me earlier.

→ Ответить