→ Pay attention
Before contest
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 days
Register now »
Rayan Programming Contest 2024 - Selection (Codeforces Round, Div. 1 + Div. 2)
4 days
Register now »
*has extra registration
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | nor | 152 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Nov/26/2024 12:21:42 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











Solution link is not open for us.
Fixed.
Thanks:)
I'm not allowed to see the solutions. Could you please fix it? I'm very interested in the solution of problem E. Thanks! :)
Fixed.
Last equality in D : aVxj - Vyi = aVxi - Vyi.
I think that's wrong because Vyi in both sides looks pretty suspicious.
Oh, try now it is fixed now
another solution for C: have a set of pair of partial sum and index of any a(i) and S that shows how many warriors died so we put S = S + k(i) then if S >= n then we put S = 0 else we get a lower_bound of(s).
(sorry for bad English)
In question D. How to check two point will be parallel?
if they are moving in the same direction with the same speed.
iff (Vxi, Vyi) = (Vxj, Vyj)
But, for example, one ghost moving with V = (2, 0) will be parallel with another one with V = ( - 2, 0). Isn't it (Vxi, Vyi) = k * (Vxj, Vyj) the condition?
We will not count those in the first place not that
aVx - Vy for the first is 2a for second is - 2a
unless a is 0, in which they will actually collide. here a >=1
Only triangle in sample in problem E? I didn't realize that the non-weighted mean of all points is not the center of mass(but it holds for triangles) the whole night!!! :(
This is a fairly non-trivial fact and I wasn't aware of it either !
Here's a useful link explaining the same.
Can someone please tell me why my code is wrong for problem Div2 C? — 37830313
I first calculated the sum of all the strengths of the warriors in the array
sum[x]. Next what I have is a value asfactorwhich is calculated based on the solution of previous round.factorbasically tells us what value from thesumarray is to be subtracted while calculating the index for next round.starttells us what part ofsumwe need to consider for this round.C1:- If the ceil search returns -1 then all the warriors are dead. Reset
factorto 0 andstartto 0.C2:- If the ceil search returns a valid
indexand value at that index is equal to the one we need, then I set thestartasindex+1i.e the index for next ceil search and the factor is calculated. Otherwise set thestartasindex(because this warrior is still alive) and corresponding factor is again calculated.You have to search such value which is sum of arrows until all warriors dead. When all warriors are dead, reset the value to 0 and repeat the previous step. Your approach is not considering about remaining helath of warrior (which is warrior[index]) in C2.
Ex) warriors : 3 2
arrows : 2 2
After first arrow is shoot, first warrior still has 1 hp. Your code might be ignoring it.
Hi! The problem is in one of the last lines, when you check
if(index-1<0). If that is true, you assignfactor = firenow. What iffactorwasn't zero? You discard all the arrows that were shooted before. I changed it tofactor += firenowand got AC. You can check my submission 37843897 :)Your code fails for cases like:
because it returns
2 2 2, but it should return2 2 1.PD: there are easier ways to code binary search (if you really don't want to use upper_bound, which is even easier) :P
Yes, my code does not follow a very clean approach, and probably this is why I overlooked this case.
Anyways, thank you for helping in figuring out my mistake. :)
You are welcome! If you want, you can check my submission to see how to solve this problem using upper_bound: 37846073. Bye!
Problem D is very amazing. Parameters: b, x[i], y[i] are useless for solving it.
Can someone please point out why this code does not work 37820945 while this code gets accepted 37840088 ,all i have changed is use vector instead of array. The non working code got stuck in some test cases and outputs only -1 for each query after a while.
Hi! The first one fails because of the arguments you are passing to upper_bound. You are using positions [1...n] of the array
a, so a[n+1] has garbage. Remember that binary search assumes the array is sorted, but a[n+1] can be lower than a[n] (we don't know what value is stored in there), so upper_bound probably does some strange things.I changed
to
and got AC. You can check my submission here: 37843999 :)
Oh thanks for pointing it out.
I tried to solve problem E by maintaining a transformation matrix T. Whenever I get a type-one query I multiply the Transformation matrix by 3 matrices, (translation, rotation, translation back) according to the rotation of the centroid around the fixed point.
But it seems that as I multiply a lot of doubles, the precision is lost. So did someone manage to solve it with the same idea but in a more precise way?
Yes, I could (using long longs though). However, I needed to move the first point to (0, 0) for more precise computation of the center of mass.
I m bit confused in theoretical proof of D question.
We assumed that two ghosts are colliding, then we found the observation that a*Vix — Viy = a*Vjx — Vjy. Means, This is the necessary condition for two ghosts to collide. But nowhere we have proven that it is sufficient codition for two ghosts to collide.
Pls, can someone prove that a*Vix — Viy = a*Vjx — Vjy is also sufficient condition for collision of two ghosts ?
It is the condition for two ghosts to collide, we found the time of collision on x axis and then checked if it is the same on y axis.
This is how to check if two moving points will meet or not.
thanks for reply, I have understood the proof. But that's only necessary for two ghosts to collide.
Initially you have assumed that two ghosts are colliding , and that's why we are comparing their corresponding X and Y co-ordinates.
but, Can we prove it reverse ? If we are given a*Vix — Viy = a*Vjx — Vjy , then prove that those two will always collide. that's what I am looking for . :) .
actually aVix - Viy = aVjx - Vjy is wrong because it also counts the ghosts that "meet in infinity (speaking physics here)".
Other words it will consider the ghosts that have the same velocity and the same direction to collide after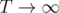 . thats why we can not start from it as it is a wrong premise that needs modification.
. thats why we can not start from it as it is a wrong premise that needs modification.
okay fine, let's say,,, we added constrain that
aVix - Viy = aVjx - Vjy where ( Vix != Vjx ) , now is it possible to proof that this is sufficient condition ?
I am asking for proof, becuase, I had found the observation
aVix - Viy = aVjx - Vjy , during the contest, but I was not able to proof that it is also sufficient, that's why I am curious, if I was missing something .
Were you able to prove sufficiency ? Even I am getting the same doubt.
check below, in reply of Jakube's reply .
I didn't exactly understand what you mean by counting ghosts that "meet in infinity". Do you mean parallel ghosts ?
a*Vix-Viy = a*Vjx — Vjy plus the condition Vi!=Vj is equivalent to the system of equations that describe a collision. Equivalence gives us both necessity and sufficiency.
a * Vxi - Vyi = a * Vxj - Vyj (III) is not a sufficient condition.
Think of it this way. From the first equation X0i + VxiT = X0j + VxjT (I) you can compute T. So if you pick this computed T, then the first equation (I) is satisfied, and if additionally (III) is satisfied, then also the second equation a * X0i + b + VyiT = a * X0j - b + VyjT (II) is satisfied (because a * (I) - (III) = (II)).
Notice, if you can't compute T from (I), then you can compute it from (II), and make the same proof, just with (I) and (II) swapped.
And if you cannot compute T from both (I) and (II), then there is no solution at all.
So two ghosts meet, whenever you can compute T (which is equivalent to Vi ≠ Vj), and (III) is satisfied.
thanks,Now I understand it :).
when we are given a * Vxi - Vyi = a * Vxj - Vy , we can say that at some time 'T', two ghosts will have same 'X' co-ordinate.
When, two ghosts, have same 'X' co-ordinate, at time T, that at that time, we can prove that they will have same 'Y' co-ordinate as well.
This is what I missed during the contest :(...
Nice solution btw. Jakube . :) . thanks a lot .
Video solution to Problem C Valhalla Siege: https://youtu.be/YuBz1keibrM
975C - Valhalla Siege
Codeforces Round 478 (Div. 2)
There's some cool geometric theory that I'm fairly sure is equivalent to what you've written for D, but at the same time is (in my opinion) very interesting and easy to miss if you just arrive at the solution through algebra.
We know that in a normal 2D plane, two non parallel lines will cross at some point. But, because of this extra time parameter, two ghosts won't necessarily cross if their intersection occurs at different times for each one. We can actually represent this geometrically by treating time as a third Euclidean dimension (i.e. Make it the z-axis). If we do that, then two intersections on this 3D Euclidean space correspond to actual ghost collisions.
Now, we notice that for two ghosts to collide, the plane spanned by their paths in 3D and the ax+b line is the same! That means we really only have to look for unique planes created by each ghosts' 3D path and the line up at time T, and count collisions for anything that isn't parallel in that plane. I'm pretty sure this boils down to calculating the exact quantities you've listed in your editorial, but I thought it was super cool how you can think about this as planes in 3D.
case :
2 1 0
-1 -1 -1
1 1 1
output :2
in this 2 ghost position (-1,-1) and (1,1), at t=1 , their position (-2,-2) ans (2,2)
so how they collide????
They meet at t = - 1.
I found solution to problem A very interesting. I didn't use bitmasks in the contest but applied it after I read the solution on here.
Here is the GitHub of all my solutions to this contest, in case anybody wants to refer them. :)
Problem E
I'm getting WA on test #4. Couldn't find the bug myself. Help needed.
Link
Hey, how does your solution for problem d make sure that ghosts with antiparallel velocities are not counted??
I assume you mean "how to make sure that ghosts with parallel velocities are not counted".
The only case when two ghosts have equal respective (aVx - Vy) 's and parallel V 's is when the two velocities are equal. So, you can compute the answer including parallel velocities and then at the end subtract 2 times the number of pairs with equal velocities.
Hmm..i get it .Thank you
The E problem is not friendly with the accuracy.
I can't pass the problem without replacing double with long double.
w(゚Д゚)w
For D, my submission 51768572 got Accepted but it gets a WA on
(it outputs -2 when the answer is 0) so maybe you should add that case.
My other solution 51767265 that also got Accepted gets WA on
54444361 please some one tell me the error it is working alright with all the possible test cases I can think of PROBLEM -C
In problem D , Lest's two ghost g1 and g2 having
velocity vectorv1 and v2 respectively.1. If v1 and v2 are not parallel then always g1 and g2 should meet at some point.2. If v1 and v2 are parallel then they should never meet(or always be together but problem says at given moment no two ghost are together).I can't figure out what I'm missing.For problem E, instead of center of mass, I keep track of the hinge co-ordinates. But it doesn't pass due to precision issues. Should there really be so much loss here ? Code