Hello!
After we successfully organized TOKI Open 2014 and TOKI Open 2017, we are going to do the similar thing this year. We will open our current IOI Selection Contest to international participants. We call it TOKI Open 2018. TOKI stands for Tim Olimpiade Komputer Indonesia, or Indonesian Computing Olympiad Team in English.
Objectives of us opening this contest include, but not limited to:
- Measure the performance of our IOI trainee compared to other countries' IOI trainee.
- Foster friendship between Indonesia and other IOI participating countries.
- Test Indonesia's scientific committee capability in setting IOI-level problems.
- Test Indonesia's technical committee capability in hosting IOI-level contests.
The contest will have very similar format with IOI, as this contest will be used to select our Top 4 and train our Top 4 for IOI. We expect that the difficulty of the contest is almost the same as IOI. Therefore, this contest is suitable for those who are preparing for IOI. The problems will be available in both Bahasa Indonesia and English.
The rules of TOKI Open 2018 are
- There will be 3 IOI-style problems for each competition day.
- You can only submit at most 50 submissions for a problem.
- You will get full feedback for each submission.
- For each problem, there are several subtasks:
- For each subtask, there are points assigned to it.
- Each subtask contains several test cases.
- You get the points from that subtask if the program passes all the test cases in that subtask.
- The score of a submission is the sum of all the points that you get from completing subtasks.
- The final score for a problem is the maximum of all the submission scores for that problem.
- Unfortunately only C++11 is supported. We will use g++ (Ubuntu 4.8.2-19ubuntu1) 4.8.2 (flags: -std=c++11 -O2 -lm) compiler
- You will only need to implement several functions described in problem statement (i.e. no I/O is needed)
- You can submit clarification requests in either Bahasa Indonesia or English.
The contest will be conducted on TLX Online Judge. You may need to register for a TLX Account if you do not have one. If you have a TLX account, you can login and go to the contest link to register for the contest. There will be two competition days, each having three problems. Each competition day will have two open windows containing the same problemset, so you can participate in either one of the window depending your time preference.
Day 1: Saturday, 26 May 2018
- Window 1: 1.30AM — 6.30AM UTC (8.30AM — 1.30PM Western Indonesian Time). Contest Link.
- Window 2: 12.00PM — 5.00PM UTC (7.00PM — 12.00AM Western Indonesian Time). Contest Link.
Day 2: Monday, 28 May 2018
- Window 1: 1.30AM — 6.30AM UTC (8.30AM — 1.30PM Western Indonesian Time). Contest Link.
- Window 2: 12.00PM — 5.00PM UTC (7.00PM — 12.00AM Western Indonesian Time). Contest Link.
A practice contest to get familiarised with TLX and the problem format is available here. The problems of TOKI Open 2017 are available for upsolving in the problem archive portal.
IMPORTANT: You are not allowed to register on both windows for the same competition day, since they will have the same problemset. If you have registered on a wrong window, you can go to the contest link to unregister.
We invite everyone (especially eligible IOI participants) to participate in this contest. See you at the leaderboard.
UPD1: The day of the second competition day is finalized. It will be on 28 May 2018.
UPD2: The preliminary result of TOKI Open Day 1 is available here. For those who registered in both windows, we only consider the score for the first window (including even if you did not make any submission in the first window).
UPD3: The post-contest blog post (includes problems repository, full result, etc.) is available here










Auto comment: topic has been updated by jonathanirvings (previous revision, new revision, compare).
Auto comment: topic has been updated by jonathanirvings (previous revision, new revision, compare).
Auto comment: topic has been updated by jonathanirvings (previous revision, new revision, compare).
Reminder bump :) The contest is less than a week away :)
Reminder: TOKI Open 2018 is less than 24 hours away :)
We have worked so hard to prepare the problems and we can't wait for the contest to start :)
looks like a nice contest :) looking forward for it
The first window of the first day of the contest has just been started! :)
Now that both windows for Day 1 have finished, can I ask about the intended approach for Problem 1?
After determining Y, I can determine X using around 340 queries. However, I have no idea how to determine Y other than brute forcing through all possibilities (random_shuffle didn't help because there are 200 tests).
I found the problems very interesting despite having only 3hrs to solve, thank you TOKI :D
My solution used 1001 queries and get 99 points.
I asked (i, i) with i from 1 to 1000, then save the result in resi. Now, a cell (x, y) may contain the treasure if both resx and resy is true. So just iterate over all par (x, y) that both resx and resy is true, and check if the data from res array is correct if the treasure was there. If it is correct, then ask another query to check if the actual location is (x, y) or (y, x).
The number of cells we have to check will be small, so this solution will run fast.
My implementation
Still wonder how to improve this (althought if I was in the official contest, focusing on other problem is definitely a wiser choice xD). I thought about not querying (1, 1) and (1000, 1000), but then I can't distinguist between (1, 2) and (5, 2).
...Now I feel dumb as fuck =(
Anyway, have you tried ignoring one random value i? It is unlikely that you choose x or y, and I think it should work fine.
Is there there is a way to mathematically guarantee that the number of cells you must check will be small for any N?
you can determine X and Y simulanteneously by querying (i,i) for all i. if for a point, you TRUE, check for the possibility that the answer is (i,x) for some x by querying the point (i,i+1). and the possibility that the answer is (x,i) similarly. Note that the number of times the second query returns false is quite rare. This approach will get 98 points. using random_shuffle and getting lucky will get 100 points :)
My approach is the following one. Ask 999 queries of the following type (ai, bi) where (a1, ..., a1000) and (b1, ...., b1000) are random permutations of {1, 2, ..., 1000}. There will be just one possible cell that is consistent with all the answers (at least with a sufficiently high probability).
The reason why such a solution works is, at least for me, quite hard to justify completely. Let me describe some facts that, heuristically, show that no more than one cell will be consistent with all queries. I am quite sure that it is even possible to choose a-priori 999 queries that identify any cell (such a choice might be the queries (1,1), (2,2), .... (999, 999) or something like that).
Fact 1: The answer to two queries that differ both on the row and the column is "almost independent" (in the sense of probability).
Fact 2: For a single query whose answer is yes, the number of cells that are consistent with the query is O(1000) (the row, the column and some more cells given by pythagorean triples).
Fact 3: With high probability there are at least two queries whose answer is true.
Hence, considering only the queries whose answer is true, we can restrict ourselves to a very small number of possible cells. Then, considering all the queries whose answer is false, we will be able to decide which one is the correct one.
I'm curious to hear the solution behind the 3rd problem. The complexity I was able to reach was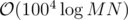 (which only gave 26 points so in the last couple minutes I wrote a
(which only gave 26 points so in the last couple minutes I wrote a 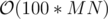 solution to get 43 points).
solution to get 43 points).
The solution is naturally divided in two steps:
The first step can be done in O(1002) exploiting the periodicity of the table both in the rows and in the columns.
Let us denote with c[r] the number of occurrences of the remainder r in the table. In the second step we have to compute the sum of all the coefficients of terms whose degree ≡ 13 (mod 100) of the polynomial
This can be done performing all polynomial computations modulo x100 - 1 that means that whenever an exponent is above 100 we do take its remainder mod 100. The result can thus be obtained through fast exponentiation (the answer will be the coefficient of x13). The complexity of the second step is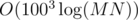 .
.
Where, or when, can I find a complete scoreboard for day 1?
Very soon. I am compiling the result (from both windows) right now :)
Original blog post updated with the URL for the (preliminary) day 1 result :)
How to solve problem B? (I guessed this is the 'killer' problem for day 1, so I didn't spend time thinking about it and focus on problem C instead.)
First off we can do a transformation of a point (x, y) to a point (x + y, x - y). Now the distance between 2 such points A, B is max(|Ax - Bx|, |Ay - By|) (this is a well known transformation so I saw it coming right when the statement provided the manhattan distance).
From this point you can initially sort by x coordinate all the points, and then you can binary search on the answer, for a total time of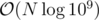 (If you want I can elaborate on the binary search, but it shouldn't be hard).
(If you want I can elaborate on the binary search, but it shouldn't be hard).
First, convert point (x,y) to (x+y,x-y). Now the distance will be max(abs(x1-y1), abs(x2-y2)).
Binary search the result, call it X. Let P be the point with minimum x. A set which contains P would be a X-by-X square with P on the lower boundary. Sweep the square along y-axis, maintain the largest distance among points not in the square. I did it by set and got TLE, had to switch to vector of prefix min/max.
A bit unrelated, but I am having trouble using the grader provided by the problemsetter. When I execute the compile_cpp, the command line doesn't print anything on the screen (I have already added the code to open the 'sample1.in' file in the grader). I had to debug my solution for problem A completely by eyes. Can anyone help me with this?
As the name suggests, compile_cpp only compiles the source code. To execute the program you should run ./name_of_problem < sample1.in (and you don't need to modify the grader).
Where can we submit the problems now?
Unfortunately you can't submit the problems now. However, you will be able to submit the problems once TOKI Open 2018 is over (i.e. after the second day)
Do the submissions get saved in the system, in case I'd want to resubmit a similar program to what I submitted during the contest? Or should I save all the programs?
The submissions do get saved in the system. You can still go to the contest URL to check all of your submissions in the contest.
The preliminary result of TOKI Open Day 1 is available here. For those who registered in both windows, we only consider the score for the first window (including even if you did not make any submission in the first window).
Where could we find the official editorials to the problems?
It will be available once TOKI Open 2018 is over (i.e. after the second day).
To all contestants: could you update your TLX account profile (https://tlx.toki.id/account/profile)? Please fill out your name and your school/institution's country.
We would like to get and share country statistics for this contest, if possible.
Thank you!
The first window of the second competition day starts in less than 15 minutes :)
How to solve day 3 — tetris?
So... how to solve Tetris?
I tried DP (L, R, x, y) which returns if we can arrange tetrominoes in [L; R] to transform state x to state y (x and y range from -1..3, storing highest two rows) but got TLE :(
If anyone's interested, or hasn't already made this deduction, here's a sketch of a proof that you can divide the board up into two-row 'states'.
The tetrominoes will be referred to as:
Let's name some states:
Each 'state' represents the top two rows of the board, at any time. The fact that the top two rows of the board will always be one of these states is proved here.
Let's firstly consider what happens when we drop each tetromino onto flat ground:
So all tetrominoes become one of these states if they are dropped onto flat ground.
Now what remains is a casebash. I'll leave out the details, since they aren't especially interesting, but I will include some important combinations of states and other tetrominoes.
The comma-separated lists are of different combinations that become the same state. For instance, the first line means both
T2' + J1 -> O'andT1' + J2 -> O'.In this case,
A + Bmeans that tetrominoBis dropped on top of stateA. The reader can confirm all of these transformations for themselves.(Obviously
O' + anythingis identical to dropping it on flat ground.)We note that these operations are all independent of whatever is below state
A— in other words, only the top two rows are important at any one time, at least for these operations. In addition, these conveniently only result in states which we have already defined.Importantly, every other combination of state and tetromino (in particular, any current state onto which a tetromino was dropped) will have a useful property: when the tetromino is dropped, it will behave completely independently of the state below it, acting instead as if it had been dropped on to hard ground. (You may also wish to confirm this.) For instance, if we look at
S'and dropT1onto it:The
S'at the bottom has been completely unchanged, and theT1has behaved as if it has fallen on to a flat ground — it has formed another 2x2 state on top ofS', and simply becomeT1'as it normally does (according to our rules for blocks falling onto flat ground).Because of these properties, then, the top two rows of the board is always categorisable as one of the states
O',T1',T2',S'orZ'given above.Thus, we note that dropping a tetromino onto any state of the board has one of the following effects:
T2' + J1andT1' + J2) result in an empty state, which corresponds to the top two rows being emptied and freeing up the two rows below them for blocks to drop on to. (This can be considered as being like 'popping off' the top state from a 'stack' of states on the board.)S' + T1example shown above. Since we've already established that every addition of a tetromino only affects the state on the very top of the board, then the state before the tile was dropped can be safely ignored.Therefore, because of these properties, in any state only the top two rows are important. This also quite naturally gives rise to the DP solution described below.
The idea works fine — you can store the highest two rows and process any changes from new blocks as they come. It seems like your solution just has too high of a constant factor.
One major optimisation to your DP is to always have state y be the empty state (so always consider only cases where the playing field is empty after the insertion of block R). The reason we can do this is that we want to end up with an empty state to solve the overall problem, and state transitions still work out fine.
In particular, our DP state is now
dp[i][j][x], and our transitions now become:i == j, we check if adding this block leaves us with the empty state, in which case by definition our DP value is true.dp[i+1][j][empty state]dp[i+1][j][changed state]dp[i+1][k][state of new top 2 rows after adding block]anddp[k+1][j][state of old top 2 rows]are true, and if so then we would be able to add a new set of 2 rows above here, and they would eventually get removed after the addition of the k-th block, by the assumption thatdp[i][j][x]is true if and only if we can end up with an empty state after adding block j.Our answer is then
dp[0][n-1][empty state], similarly to your solution. (Technically we have to keep track of some extra stuff to actually solve the problem, since we need to output the rotations, but those are implementation details.)My approach is DP(L, R, state) which returns true if we play these tetrominoes independently and result in an empty slot or a slot with 2 rows; got accepted sub 4.
UPD3: The post-contest blog post (includes problems repository, full result, etc.) is available here