Всем привет, хочу с вами поделиться интересной задачей и классной идеей.
Необходимо реализовать структуру данных, выполняющих 2 типа запросов:
- Изменить элемент в массиве
- Найти сумму различных элементов с L по R.
Например массив выглядит так: { 1, 2, 1 }, тогда сумма различных от 1 до 3 равна 3
Для начала разберем "лобовое" решение задачи за 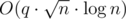 с помощью корневой оптимизации. Спасибо Holidin, который объяснил мне это решение.
с помощью корневой оптимизации. Спасибо Holidin, который объяснил мне это решение.
Построим персистентное ДО для суммы различных элементов на отрезке. Заведем еще одно ДО с unordered_map<int, int> в вершине, которое хранит количество элементов, равных X на отрезке.
Ещё будем накапливать до  изменений, если из стало
изменений, если из стало  , то перестроим наше персистентное ДО заново за
, то перестроим наше персистентное ДО заново за 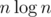 . Чтобы ответить на запрос суммы на отрезке, посчитаем ее с помощью первого ДО, затем пройдемся по всем накопленным изменениям и проверим, входят ли они в наш отрезок и как они меняют сумму с помощью второго ДО с map'ами. Ответ на запрос будет за
. Чтобы ответить на запрос суммы на отрезке, посчитаем ее с помощью первого ДО, затем пройдемся по всем накопленным изменениям и проверим, входят ли они в наш отрезок и как они меняют сумму с помощью второго ДО с map'ами. Ответ на запрос будет за 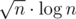 .
.
Теперь решим задачу нормально за 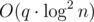 в онлайн.
в онлайн.
Для начала пусть нам надо просто считать количество различных элементов на отрезке с изменениями.
Ключевая идея: пусть для каждого элемента мы знаем next[i] — индекс следующей позиции j, такой, что a[i] = a[j], i < j. Тогда количество различных элементов на отрезке [L; R] равно количеству элементов на том же отрезке, у которых next[i] больше R.
Тогда решение очень простое: построим ДО, в котором можно будет считать количество элементов на отрезке [L; R], больших R, для этого в вершине будем хранить ДД по ключу(next[i]). Чтобы обновлять next[i], я лично поддерживал map<int, set>, элемент которого m[x] означает множество позиций, на которых стоят x.
Теперь вернемся к нашей задаче. Чтобы добить её, нужно в декартаче по ключу(next[i]) хранить сумму a[i] в поддереве.
UPD: Ссылка на задачу Спасибо kefaa и khadaev











link