Endagorion's blog

Разбор VK 2018 Round 3 + Codeforces Round #477
By Endagorion, history, 7 years ago, translation, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial of VK Cup 2018 - Round 3
  • Vote: I like it
  • +83
  • Vote: I do not like it

Comments Comments (13)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In the first line of the solution to Div1.D, does the word "formualate" mean "formulate"?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

for div 1 C i chose greedily the minimum value with which we should xor so that we can find the next value in a which is greater than the previous value. I used trie with deletion. Here is the code . http://codeforces.me/contest/967/submission/37730673. Why doesnt it work ?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In 967B — Watering System, if we are sorting the holes, shouldn't the complexity be O(n * log(n)).

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +10 Vote: I do not like it

    Sure, it should be O(nlogn) were we using a comparison based sort. Here though, we can use a linear time sorting algorithm such as counting sort. The complexity in that case would be O(n).

    → Reply
»
7 years ago, # |
  Vote: I like it +11 Vote: I do not like it

Can someone explain div 2E ? Not able to understand from editorial.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Well, I think div2 E is really an instructive problem though I can't figure out the solution during content.

    First, Let's define some functions that can be used in my explanation.

    Let P(x) denote the position of leading bit of x, 0-indexed. (You can also consider P(x) is the length of x (binary representation) minus 1). Formally, if x is in the range [2k, 2k + 1), then P(x) = k. For example, P(5) = 2, since the leading bit of 5(101b) denotes 22.

    Let F(x, n) denote the nth least significant bit of x, 0-indexed, or, the nth bit from right in the binary representation of x. For example, suppose x = 13, then F(x, 0) = 1, F(x, 1) = 0, F(x, 2) = 1, F(x, 3) = 1, since 13 = 1101b.

    Note that F(x, P(x)) is always 1.

    Then, Let's consider a basic problem. Suppose we have a sequence a1, a2, a3, ...ak meeting the strictly increasing condition and the current xor sum is s. We are going to append a number x to the sequence, making a new xor sum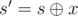 . In which condition, the sequence after appending x is still strictly increasing, or, in other words, s' > s?

    The answer is easily to find. if and only if F(s, P(x)) = 0. For example, if x = 5 = 101b, to make sequence increasing, the 22 bit of s should be 0. If s = 1101b, the 22 bit is 1, then after xor x, the 22 bit will be set to 0, making the sequence decreasing.

    So we can get such a solution for div 2E. Initially, we consider the sequence is empty and s = 0, and select a number x in all n numbers which meets the condition F(s, P(x)) = 0. Then append the number x to sequence and update s. Repeat n times, the answer is got.

    However, when there are more than one number that is able to select, which one should be selected first? The answer is simple. Just select the one with least P(x).

    For example, if the current s = 1010b, and we have two numbers x1 = 101b and x2 = 1 to select. P(x_1)=2, P(x_2)=0. So we should select 1. Why?

    Because if we first select x2 = 1 (the one with less P(x)), it will not modify the most significant bit of x1 in s , in other words, F(s, P(x1)) will be change by the operation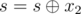 . So that we can append x1 after appending x2.

    Otherwise, if x1 is selected first, s will become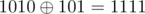 , then we can't append x2.

    Last question, if there are more than one number that is able to select and has least P(x), which one should be selected first? The answer is that it doesn't matter. In that case, we can choose any one of them. Why? Remain for thinking.

    Here is my solution:37857270

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      thanks a lot for sharing this :)

      → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I didn't get the last part,when there are more than one options to choose from,you said we have to choose the one with least p(x),because if we append the one with higher p(x),it may change some zeroes to ones,leaving less "space"(zeroes) for the next number to append.

      But there can be only 60 bits,and there will be 100000 numbers,so some of the ones should also get converted to zeroes for the solution.So how does it matter then?

      → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

for Div. 2 D i cannot find any special test case in which this type of thinking is wrong : First we can binary search the minimum k1 such that the value of the smallest element >= x1 / k1, after that we can just sort the vector and remember the initial positions of the elements that so we can just verify that the (k1 + 1)-th element >= x2 / (n — k1), because n — k1 is the maximum number of elements for the second service that we divide x2 by. If the inequality is correct then we can just output the solution(meaning we output the indices of elements in the vector because we stored them). Do the same by finding the minimum k2. If you find no solution output No. I think this solution works great because after we sort the array and we make the groups if the smallest elements of the groups respect the condition of value >= x / k then the rest of the elements will respect it, and the smallest element needs to be in a group also, so we can just find ki(where i is 1 or 2, we analyze both), then to be sure that we can build the other group we can find the most suitable case to be biggest n — ki, so we cam=n binary search ki, and to have the largest numbers, so by the observation we made earlier, we can just grab the smallest elements for this group after which we get the most suitable condition, so we get a O(N + log2(N) * 2) = O(N), but i get a WA on test 5 ! can somebody please help me ? This is my submission 39044055

→ Reply
»
10 months ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

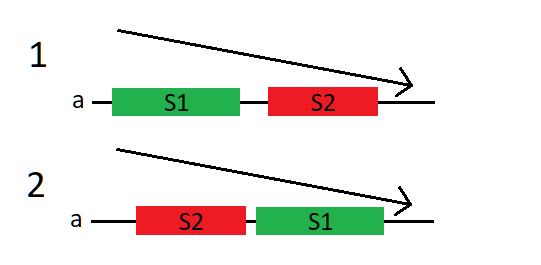
I could solve Div2B — Resource Distribution greedily. Sort all servers in decreasing order (don't forget about original indices). It's optimally to select two contiguous subsegments of servers for each service.

Consider a case when servers for service $$$S_1$$$ are with greater specifications than for service $$$S_2$$$. Take servers for $$$S_1$$$ greedily. Let's $$$k$$$ is number of selected servers, hence we select $$$k$$$ greatest servers and $$$a_{k-1}$$$ is least of them. Find least $$$k$$$ that $$$\lceil \frac{x_1}{k} \rceil \leqslant a_{k-1}$$$. Then remove first $$$k$$$ elements and repeat this for service $$$S_2$$$.

If there's impossible select servers for $$$S_1$$$ or $$$S_2$$$, begin from $$$S_2$$$. Try both cases. Don't choose service with greater $$$x$$$.

→ Reply