apoorv_kulsh's blog

Divide by Zero 2018 and Codeforces Round #474 (Div. 1 + Div. 2, combined) Editorial
By apoorv_kulsh, 7 years ago, In English
Tutorial is loading...

Set by : vntshh

Setter's solution
Tutorial is loading...

Set by : AakashHanda

Setter's solution
Tutorial is loading...

Set by : 7dan

Setter's solution
Tutorial is loading...

Set by : Vicennial

Setter's solution
Tutorial is loading...

Set by : rohitranjan017

Setter's solution
Tutorial is loading...

Set by : kr_abhinav

Setter's solution
Tutorial is loading...

Set by : apoorv_kulsh

Setter's solution
Tutorial is loading...

Set by : arnabsamanta

Setter's solution

Do give your feedback here : https://goo.gl/forms/xbsdMxnkA3XsG4092. Would love to hear your feedback, since that would help us get better!

  • Vote: I like it
  • +63
  • Vote: I do not like it

Comments Comments (38)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by apoorv_kulsh (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by apoorv_kulsh (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Really good problem set.

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -9 Vote: I do not like it

Solution for C is suboptimal, you can greedily choose the greatest K such that 2^K-1 <= X.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it -10 Vote: I do not like it

    The array should have exactly X subsequences.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    You don't need to output an array with minimum number of elements. You just need to find any array with size ≤ 104. There may be a different solution than described here, which is able to produce an array with lesser number of elements and satisfying the constraints.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem F, I created another graph with edges as vertices and then ran DFS on it. My solution is exceeding memory limit and I couldn't optimize it furthur. Please help. http://codeforces.me/contest/960/submission/37094773

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +3 Vote: I do not like it

    At the bottom of your submission there is the part of the test your solution got MLE. As you will notice, the test contains 1e5 self loops. The problem is that for such a graph, by turning edges to nodes, you make new graph with |E|2 edges, thus your algo total complexity is |E|2 which is too much and the memory you take then is |E|2 too, which caused MLE before TLE :<.

    edit: notice that the problem still exists in usual graphs without self-loops. That's why switching vertices with edges is possible only if every vertex has small degree, cause every vertex causes his adjacent edges to form a clique, when you transform the graph

    → Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Can someone explain to me how to write Dynamic Segment Tree in O(n*log n)? Is it possible to do it iteratively? Thank you in advance!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    I usually do segment tree recursively. The way you use this structure is the same, but, instead of creating all nodes, you just create nodes that you actually need (you do not need a build function, only update).

    Suppose that you will insert/update something on index 5 and left node keep values in [0, 5], there is no need to worry about right node.

    It's kinda of more complex, but you can do this with lazy propagation too.

    My submission on F: 37069514

    → Reply
»
7 years ago, # |
  Vote: I like it +6 Vote: I do not like it

Video solution to Problem B: https://youtu.be/s_qtv8MisbQ?t=3m13s

960B - Минимизация ошибки
Divide by Zero 2018 and Codeforces Round 474 (Div. 1 + Div. 2, combined)

→ Reply
»
7 years ago, # |
  Vote: I like it +22 Vote: I do not like it

Amazing problemset. Although in my opinion, problem F is much easier to write than problem E :)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +14 Vote: I do not like it

    We apologise for the scoring issue. We underestimated/overestimated a few problems.

    Glad to hear you like the problem set :)

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For F my O(n) soln is giving TLE http://codeforces.me/contest/960/submission/37123425 can anyone help please

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    In F your solution is quadratic in the worst case, when all the edges are between the same two nodes. Check the case you got tle on

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please tell me why I got tle in question F Link to my code http://codeforces.me/contest/960/submission/37079088

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    maybe you are making same mistake as i did..read reply on my comment above

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why dynamic segment tree is required in problem F? Can't it be solved with static segment tree? Can anyone help me where I am going wrong?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 4   Vote: I like it +6 Vote: I do not like it

    Sorry for my poor English: It is possible solve it with static segment tree: For every edge that goes from node u to node v add this in a list of edges that leave the node u, then in every node the edges are ordered, because you add this in the same order of the input and in every node have a segment tree of max, that store the max length of a path that end in this edge, it is easy to see that the sum of all edges for every node is M, because every edge is added to only one node, then initially the length of all the path for every edge is 1, in other list that contains all the edges sorted by minimum weight process the edges now, what happen when a edge (u, v, w) comes, it is possible to traverse along this, then update in node v all the edges that comes after the current edge in the input with x=value of this+1 we obtain this value doing a query to the segment tree in node u for the position of the current edge, the position (p) of the first edge that comes after the current edge is possible search it by a binary search in the list of edges of node v, then update the range (p, end) with x, every time that you process one edge update the answer, only left one problem: what happen when a edge of weight w update other after(in the input) with the same value w, this is violating that the weights of the path is strictly increasing, to solve this, store the value of all the next edges to process of the same weight w, used this value to update, so not matter that you update "invalid" edges weight lower or equal to the current because this values never will by used when you process the edges sort by weight Finally let you a link to my solution: 37110519 It is possible solve with a unique segment tree you only assign for every edge in the same node a continuous position on it.

    → Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Nice editorial especially problem D

→ Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

HDU4372 960G - Бандитский блюз

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem G, how did you do FFT by modulo? Can you explain it more detailed? I know that it is because MOD-1 is divisible by 2^23, but what it gives to us? And where did you get numbers root and root_1?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

For problem G, is there some intuitive way to realize that number of permutations with |LIS| = k k elements visible from front is in fact just Stirling numbers of first kind? (It is evident from the recurrence, but not able to create a mapping between the two)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    We can solve the problem as follows:

    For each i from 0 to n, find the number of ways we can permute i elements to have exactly a - 1 records lets call it f(i, a - 1). In the end , we can select f(i, a - 1), f(n - 1 - i, b - 1), and we place n between them to make it exactly equal to (a, b) records.

    We can find that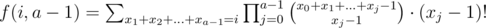 using basic combinatorical interpretations.

    Now, also .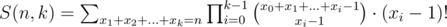

    So, f(i, a - 1) = S(i, a - 1).

    Now, to find final answer you can use the formula mentioned in the editorial, and here

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 3   Vote: I like it 0 Vote: I do not like it

      Thanks, but that's not what I asked. I already know that their recursion formulas (and polynomial form) are identical.

      What I'm looking for is an intuitive explanation which tells why is the number of permutations with exactly k cycles (i.e Stirling numbers of first kind) equal to the number of permutations with |LIS| = k elements visible from front. Is there some explanation which is able to map number of cycles to number of elements visible from front?

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      On an unrelated note, can you elaborate on "using basic combinatorical interpretations." please? How do you come up with that formula?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +5 Vote: I do not like it

        We can build each permutation of n elements having k records as follows :

        Express n as sum of k positive integers, x1, x2, ...xk. Now, repeat k times :

        • Create a new block of size xi, place the largest available element to the leftmost position of this block, and select and permute the rest available xi - 1 elements arbitrarily.

        Append this block to the left of the previous block.

        The number of ways to select elements for the ith block corresponds to the ith binomial coefficient in the product, and the factorials for internal permutations.

        We iterate over all ways to express n as a sum like this.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          Nice!

          This explanation also helps realize the equivalence between number of cycles and size of LIS number of elements visible from front.

          x1, x2, .. xk can correspond to the size of the K cycles. The largest element of each cycle corresponds to an LIS element.

          → Reply
»
6 months ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it 
//DP solution for problem B. I wasn't able to prove that greed would work. That's why DP came to my mind 
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define all(a) a.begin(), a.end()
#define nline '\n'
#define debug(x) cout  << #x << ":" << x << nline;


ll performOperation(int index, int num_operations, vector<int>&d) {

    if(num_operations <= d[index]){
        return (1LL*(d[index]-num_operations))*(d[index]-num_operations);
    }
    if((num_operations - d[index])%2 == 0 )
        return 0;

    return 1;
}

void  solve(){

    int n, k1, k2;
    cin >> n >> k1 >> k2;
    int k = k1+k2;
    vector<int>a(n+1);
    vector<int>b(n+1);
    for(int i = 1; i <= n; i++){
        cin >> a[i];
    }
    for(int j = 1; j <= n; j++){
        cin >> b[j];
    }
    vector<int>d(n+1);
    for(int i = 1; i <= n; i++){
        d[i] = abs(a[i]-b[i]);
    }
    vector<vector<ll>>dp(n+1,vector<ll>(k+1,INT64_MAX));
    for(int j = 0; j <= k; j++){
        dp[n][j] = performOperation(n,j,d);
    }
    for(int i = n-1; i >= 1; i--){

        for(int j = 0; j <= k; j++){

            ll mini = performOperation(i,0,d) + dp[i+1][j];
            for(int x = 0; x <= j; x++){
                //perfrom x operations on 'i' and perform 'j-x' opertion form i+1;
                ll operations = performOperation(i,x,d) + dp[i+1][j-x];
                mini = min(mini,operations);
            }

            dp[i][j] = mini;

        }
    }

 

    cout << dp[1][k] << nline;
};

int main(){

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);cout.tie(NULL);
    solve();
}[problem:960B]
→ Reply