Atcoder Grand Contest 022 will be held on Saturday (or Sunday depending on your timezone). However, the time of this contest will be three hours later than the usual time for Atcoder contests, i.e. 12am JST instead of 9pm JST. Thus, please check the contest time carefully here.
I (zscoder) am the writer of this contest and this contest counts for GP30 scores.
Duration : 150 minutes (2 hours and 30 minutes, 40 minutes longer than usual)
Scoring Distribution : 300-600-700-1600(1000)-1600-1600
I hope you will enjoy the problems. Although the date of the contest is 1 April 12am JST, it is assured that this contest is not an April Fool joke :)
Let's discuss problems after the contest.











Does it intersect with CF April Fool's?
Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
Codechef March Lunchtime clashes with it :(
Auto comment: topic has been updated by zscoder (previous revision, new revision, compare).
Contest starts in < 1 hour.
Duration: TBD.
Really?
They probably forgot to update the blog. It's confirmed to be 150 minutes.
When you make the mistake of picking Codechef LTIME over it and it gets cancelled...
just curious, why didn't you just switch over?
Bleh I just started thinking about the CC problems and felt too lazy to start a new contest.
https://oeis.org/A214765 Is problem F this?
No, the fifth term doesn't match.
No, we oeised the sequence and it wasn't found.
Wow, I had never used Atcoder until today. It's an amazing platform! 10/10 loved it <3 really, try it out.
My idea for B was to select x elements which are multiples of 2(and not 3), where x is multiple of 3. Select y elements which are multiples of 3(and not 2), where y is multiple of 2. Other elements are multiple of 6. Then, for all elements which are divisible by 2, you get GCD as 2, and so on. But my solution is passing only half of the test cases. Can anyone please help me out? Here is my code: https://pastebin.com/PqdrRxD5. Is there any way of downloading the test cases?
Testcases are published at https://atcoder.jp/post/21.
Thanks a lot! My approach was completely wrong :(
Your approach is almost fine. I used the same, but selecting x elements which are multiples of 2 and not 3, with x a multiple of 3, is not sufficient.
For example you might pick (2, 4, 8). Their sum is 14, and not divisible by 3.
To make your approach work all you have to do is make sure that you have x elements which are multiples of 2 and give 1 modulo 3 and also x elements which are multiples of 2 and give 2 modulo 3. That's how you ensure the sum is divisible by 3.
I got AC with that.
Here's a method for B that was easier to code:
Even though Japanese blood doesn't flow within zscoder, tasks were, as always on AtCoder, great.
zscoder watches anime to make up for that
It looks like problem D has weak testcases. I just took O(n2) DP (like in editorial) and bound the second parameter by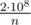 .
.
Also was it intended in problem F that any polynomial solution is OK? I had O(n6) and it was OK to precalc (actually it works about 4s, so probably even with O(n7) solution you can do precalc).
Yes, I'm sorry for the weak testcases for D. I tried hard to fail some wrong greedy solutions but am not aware that bounding the parameter of the O(n2) dp passes.
Also, it is intended for F that any polynomial solution that you can precalculate in time to pass. Initially, the constraints were set to N ≤ 100 but we decided to lower it to N ≤ 50.
Anyway, congratulations on the win.
I found the second question on constructive algorithm quite random.Any insight on how to approach such problems.
I have one general question about problems like problem E: how to solve this type of problems? It can be easily seen that you need to find out correct pattern for good (or bad) strings. I do some pen-and-paper work trying to find useful properties of good strings or guess the pattern. Sometimes it works, but not always.
Try out small cases and also find some observations (invariants, necessary conditions etc...). For example, for this problem, I noted that if the string has 4 or more consecutive ones, then it must be beautiful, and so we only need to consider strings with ≤ 3 consecutive ones. It also helps if you wrote a brute force and print out all possible small cases to either analyze the pattern or verify your conjectures.
For this particular question I observed a few greedy rules that help me reduce strings. For example it is always good move to replace 000 with 0. I analyzed problem a bit more and observed more such rules and then concluded that there is finitely many equivalence classes of prefixes and I can identify them with partially reduced strings. For example, if I'm dealing with prefix and I don't know my future, I know that if I see 001 I can reduce it to 0, but I can't reduce 100 to 0 because 0 may come next. Or when put in other words, this can be simulated by constructing an automaton and counting number of partial paths ending at every state. My automaton had 10 states, but I didn't built it explicitly, I just had map<string, int> dp and function string Reduce(string) that searches for patterns that can be greedily reduced.
However I don't think this is a general way of dealing with such problems, I found my approach pretty unique. I did not try to find some general way of describing good strings (or, I tried but failed) and I don't think bruteforce would have helped me to observe any patterns.
Wow, that's awesome.
The time was so unusual and I just noticed it.