Hi all,
The US Open and final contest of the 2017-2018 USACO season will be running from Friday, March 23rd to Monday, March 26th.
As always, please wait until the contest is over for all competitors before discussing any specifics of the contest here.
Update: The contest is now live! Good luck to all competing!











JOI TST 2018 + COI 2018 + USACO Open 2018 + NAIPC 2018 + VK Cup 2018 R2 + ARC 093. Six contests in this week!
More like this weekend.
Auto comment: topic has been updated by xiaowuc1 (previous revision, new revision, compare).
Can we begin discussion?
After 2 hours and 40 minutes, yes.
Very Accurate Depiction of True Events
damn xD
You're joking but seriously how to solve platinum P2?
I think I have a theoretical solution. I haven't coded it up yet but I'm pretty confident it would work.
If K ≤ 2000 it can be solved using your favorite sliding window RMQ, so we only need to consider the case when K > 2000.
First divide the numbers into blocks of 1000. In the first pass, compute the minimum of each block.
On the second pass, we handle the queries. Each query will contain part of a block (prefix), one or more whole blocks (body), and part of a block (suffix). The minimum will be the minimum of the minimum of the three sections.
In memory, we store all the numbers in the block containing the prefix and all the block minimums.
We don't know what the minimum of the suffix is but we do know that it is at least the minimum of that block. So, if the minimum of the prefix or body is smaller we just output that and move on to the next query. Read in another block if the prefix runs out.
The tricky case is if the minimum of the block containing the suffix is smaller than the prefix or body. However, notice that in 1000 queries, we will read in a number that is less than any other we currently have. This means that when we read it in, we can discard everything in all blocks before it (similar to monotonic queue).
To handle the 1000 queries before that happens, we first read in the block after the prefix as a buffer. Then, we skip everything until we reach the suffix and read in the suffix. Now we can actually handle the queries: using the prefix, body minimums, and suffix. The buffer makes sure the prefix doesn't run out in the process. Once the right end of the queries reaches the end of the block containing the suffix, we will know that we read in a new minimum, and can discard everything except the block minimums and suffix elements. We are now back in the original state.
Can anyone explain solutions for platinum P1 and P2?
Here is my code for P1, I think it's rather simple to understand solution:
https://ideone.com/agAsKt
I have not enough time to implement P2, my solution is very complicated and I couldn't well implement self memory management using 5500 mem cells :(
Any brief proof of correctness / logic on why this works?
.
It's a little bit difficult for a non-native speaker to explain the idea, but I will try :-)
So, the algorithm is: For each value of x, COUNT THE NUMBER OF VALUE GREATER THAN x IN THE INITIAL SEGMENT, and if there's exists one value SMALLER than x placed after x, the counter is increased by 1 (because of extra bubble phase)
Can someone check out my code for Plat P3 that uses HLD based on this blog post?
I was only able to get TC 1 and WA on the rest. :(
You don't actually need a segment tree for the chain update part.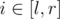 " right?
" right? , so the total complexity becomes
, so the total complexity becomes 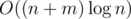 instead of
instead of 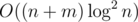 (plus possibly many bugs).
(plus possibly many bugs).
All your updates are "Do ai = min(ai, x), for
But as your queries are sorted by x, you can rephase your updates as "Set ai = x, if ai is currenty unset". Because if you've set a index before, that will mean it is already less than your current x.
By this way, you can just keep a set of unset indexes and find the indexes which lie in range [l, r] and update them. In total you'll make
@RezwanArefin01 lol I did realize that when I was posting my code up, but I decided to keep it as is because the issue is WA not TLE.
How did you do Gold P1 and P3?
For P3 I did knapsack where the dp[i] is minimum weight in knapsack with talent i.
It is guaranteed at least one dp[i] > W, so there will always be a solution.
For P1 I haven't found a way to solve the backwards case, it it really hard >:(
Did you get AC with your code? Here is a simple test which gets WA: ideone
Some minimum weight with talent i is not guaranteed to be > W, only some weight is guaranteed to be > W?
Yeah I got AC in contest.
As for the test case:
120/7 = 17.1428...
we multiply by 1000 and it's 17142.8..., and then we floor it.
17142 is correct.
Also there is guaranteed to be the case where we choose every cow (dp[mxTalent] > W).
Code?
https://pastebin.com/bCtzScRY
I think it's a bit simpler than the editorial — but slower
dp[i] minimizes weight for talent i, not maximize talent for weight i (comment is incorrect)
Problem 3: https://pastebin.com/bCtzScRY
It says "maximize talent" but it really means "minimize weight", it originally did 0-1 knapsack with weight and maximized talent but realized the time/space would not fit so did it reversed.
Results are out.
My brute force on Plat #3 still gets 14/15 test cases. :P
Oh, haha nice! I spent nearly 2 hours trying to fix a memory issue with my solution to Plat #3 to no avail. But after results came out it strangely got full score (which was nice of course)... unfortunately I don't get my 2 hours of debug back :(
Somebody also told me that plain loop + #pragma gets AC :(
If we add n=1 case in platinum P1 , many participants' solutions including author's one would be failed. The correct output should be 0 (because length(A)=1) but author's solution outputs 1.
OMG I think you're right. But most people would probably realize and fix it if it was included. :)
Thanks for pointing it out! My solution should now be fixed.
can someone help me debug for plat #3 plz. getting some weird runtime errors for the last few test cases (got cucked by regrading)
jk plz ignore, not a runtime error, but memory limit exceeded :| (solved)