Hello. Suppose you have n boxes and there are a[i] balls in the i-th box. In one operation you can choose 2 balls from 2 different boxes and throw them. Is it possible to perform some number of operations such that in the end a[i] = 0 for all i? I know that the answer is yes iff a[i] <= s/2 for all i, where s is the sum of a[i]. But why is this condition sufficient? I understand that its not possible to make a[i] = 0 when a[i] > s/2, but why does this guarantee that we will be able to reach the state where all a[i] = 0? Thanks in advance.
→ Обратите внимание
До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
14:07:41
Зарегистрироваться »
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
14:07:41
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3993 |
| 2 | jiangly | 3743 |
| 3 | orzdevinwang | 3707 |
| 4 | Radewoosh | 3627 |
| 5 | jqdai0815 | 3620 |
| 6 | Benq | 3564 |
| 7 | Kevin114514 | 3443 |
| 8 | ksun48 | 3434 |
| 9 | Rewinding | 3397 |
| 10 | Um_nik | 3396 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 155 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 10 | djm03178 | 152 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 30.11.2024 03:27:20 (i1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










Proof by induction: Always throw balls from the 2 boxes with most balls, this preserves the a[i]<=s/2 (both a[i] maxes are reduced by 1, s/2 reduced by one, other a[i]'s can't have >s/2 without any of them being the max previously).
Obviously this will only work if you have an even number of balls. Otherwise there will be one ball left at the end.
One method that works is: pick the two boxes with the most balls and remove a ball of each one.
It is easy to see, that when you have still some balls in some boxes, and the inequality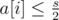 holds for all i, then you can always perform this operation because you have at least two non-empty boxes.
holds for all i, then you can always perform this operation because you have at least two non-empty boxes.
The thing left to prove is, that after one operation the inequality still hold. Of course now with s - 2, since we removed two balls: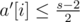 , where a'[i] is the modified array after the operation.
, where a'[i] is the modified array after the operation.
And that's also easy to prove. If there are any boxes with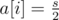 before the operation, then there are at most 2 of them. So you will remove one ball from each of those, and after removing you have
before the operation, then there are at most 2 of them. So you will remove one ball from each of those, and after removing you have 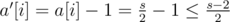 .
.
All other boxes have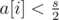 before the operation, so they are already
before the operation, so they are already 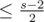 and this obviously doesn't change by performing the operation.
and this obviously doesn't change by performing the operation.
So to recap: If you are in the situation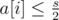 for all i, then you can perform the operation and end up in the exact same situation. Therefore you can reapeat this as long as you have any balls left. And since you don't have any balls left at the end, all boxes are empty.
for all i, then you can perform the operation and end up in the exact same situation. Therefore you can reapeat this as long as you have any balls left. And since you don't have any balls left at the end, all boxes are empty.
Thank you very much. Got it.