Greetings to the CodeForces Community!
The February Long Challenge is just around the corner and I would like you to be a part of it. With 10 programming questions spread across 10 days, you can participate and solve all of Chef's puzzles. Joining me on the problem setting panel, we have:
- Problem Authors: I_love_simplespy (Zhuolin Yang),markysha (Mark Korn), kamranm (Kamran Maharov), chemthan (Trung Nguyen),nerdyninja (Omkar Prabhu),payback_1996 (Ankit Raj),shivam010(Shivam Rathore)
- Problem Tester: Ioser (Hanlin Ren)
- Russian Translator: CherryTree (Sergey Kulik)
- Mandarin Translator: huzecong (Hu Zecong)
- Vietnamese Translator: Team VNOI
- Editorialist: Ioser (Hanlin Ren)
- Statement verifier: Xellos (Jacub Safin)
- Admin: kingofnumbers (Hasan Jaddouh)
I hope you will enjoy solving the problems. Please give your feedback on the problem set in the comments below after the contest.
Contest Details:
Time: 2nd February 2018 (1500 hrs) to 12th February 2018 (1500 hrs). (Indian Standard Time — +5:30 GMT) — Check your timezone.
Details: https://www.codechef.com/FEB18
Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.










Auto comment: topic has been updated by Ioser (previous revision, new revision, compare).
Auto comment: topic has been updated by Ioser (previous revision, new revision, compare).
MemS your editorial in the sept17 contest were great. Hope for the same. :)
This isn't MemS. He is yellow :O
Wow, really excited to see author from my country! Great job kamranm.
Thank you. ) I hope you will enjoy the problems.
How fast is the CodeChef's judging server? Is it as fast as Codeforces' judging server?
I think it's a bit faster than codeforces, about 1.2 times.
I believe that that statement is a bit controversial. While Codechef's judge has significantly improved, it still judges 2x slower than Codeforces's judges when there are long queues and only just equals Codeforces's when the queue is small.
Does that mean a solution could get TLE when the queue is large and get AC when the queue is small?
Can you please tell where did you notice that and we will investigate it if it turned out to be true.
Reduce time of other language such pypy and pyhton for problems.
Is it possible somehow to contact CodeChef admins regarding wrong institution name on Codechef? I did not get any personal response from [email protected] and [email protected].
Hello,
We are looking for people to write editorials of Codechef problems, if you are interested please apply in this email: [email protected], please identify yourself and include anything that can encourage us to assign you as editorialist.
requirments:
1- Editorialist should have good writing skills and know how to orginize ideas
2- Editorialist should be high rated competitve programmer because he has to understand solutions to difficult problems
3- Editorialist should be responsible and provide editorials on time
4- Editorialist should be able to provide very high quality of editorials, example of typical editorials: link1, link2, link3
Compensation:
Long challenge: 300$ for editorials of all problems
Cook-off: 150$ for editorials of all problems
Lunchtime: 150$ for editorials of all problems
What about challenge problem? Should editorialist write solution which gives a good score (like 70-80)?
Editorialist is not required to come up with solutions himself (generally speaking, not only challenge problem), he can seek help from problem setter/tester but he should be good enough to be able to understand the solution.
For problem CHANOQ, is there a chance for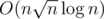 solution? I thought this was a pretty easy problem for a level 7 until I get TLE...
solution? I thought this was a pretty easy problem for a level 7 until I get TLE...
I sorted the segments in the increasing order of left endpoint, then divided them into block, and for each of the block, I sorted the segments in the decreasing order of right endpoint. Then, for each of the point, I can update the parity of all the segment in
block, and for each of the block, I sorted the segments in the decreasing order of right endpoint. Then, for each of the point, I can update the parity of all the segment in 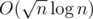 .
.
My code
My solution
Basically it solves the problems separately for queries with one point, two points and 3 or more points. The first two cases can be easily solved with segment tree, and the last one means that there are no more than
2e5 / 3such queries, and it can be solved with bitset within the memory limit for O(n2).I solved it with square root decomposition (AC), with the following algo:
If the number of points in input query are greater than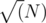 , then do brute force in O(N). There can be no more than
, then do brute force in O(N). There can be no more than 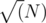 such queries, so complexity for this part is
such queries, so complexity for this part is 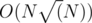 .
.
If the number of input points is less than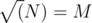 , then do
, then do 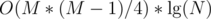 with persistent segment tree. Note that
with persistent segment tree. Note that 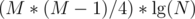 is less than
is less than 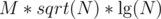 . Also,
. Also, 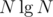 pre processing is required for PST.
pre processing is required for PST.
My Code.
can you please explain the persistent segment tree part a little more. It will be a great help for the beginners like me :) Thank you!
Actually in the ith segment tree, we update for all segments having left point ≤ i, leaf node = r[i] + = 1. This is the pre-processing.
Then , we can easily answer in O(logN), number of segments having left end point between l...r and having right end point between s...e.
The overall complexity is still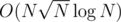 with a lower constant factor, right?
with a lower constant factor, right?
PS: Oh right, if we set M a bit lower than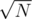 , the running time will be reduced.
, the running time will be reduced.
You can also solve it in O(M*(N/32)) in a very short code using bitset and exploiting codechef's memory limit.
Code
It's funny how this solution run even faster than MazzForces's solution.
Bitset is really overpowered...
A trick is to let the size of block be something like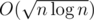 or
or 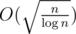 so that time complexity becomes
so that time complexity becomes 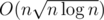 rather than
rather than 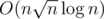 . (Hey, a
. (Hey, a 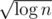 speedup!)
speedup!)
Another trick is to choose the constants before block size carefully.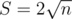 and
and 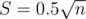 are usually very different. This is better done by experiments.
are usually very different. This is better done by experiments.
can someone please explain how to solve "chef and Land labelling" problem.
Greedy works. Find all candidates for each row and update row with minimum number of candidates. Don't forget to delete non-proper candidates of other rows after giving label to some row.
Code: https://www.codechef.com/viewsolution/17404392
To admins, testcases of this problem are weak. My solution is O(n3) which can be decreased into O(n2logn) very easily, but it still gets accepted.
if you don't mind then can you please elaborate your solution.
For finding candidates for each row, we need to don't consider 0's in the matrix, so we keep each row in v[i]. Let can[i] be set of candidates for row i. For each x, we consider x as candidate of row i if permutation created by x is some rearrangement of row i.
Now we need to sort can[i] by size of its set (its hypothesis of our greedy). For that, we make another set s and keep id and size of each can[i].
We know that answer is always possible, so we do following operations exactly n times: Select first element of s (which has minimal count of numbers in can[id]) and update its label with any of numbers in can[id].
We also know that d[gcd(label[i], label[j])] = arr[i][j] if d[x] is count of divisors. So, for each i, d[gcd(label[id], label[i])] = arr[id][i] and we know id (which is t.S in above code). Therefore, we need to delete "bad" numbers from can[i] set for each i. For finding this "bad" numbers needs iterating can[i] set and deleting something while iterating set doesn't seems good, so make new array and push there bad numbers, then delete them.
LUCASTH: Use dp/bruteforce for finding values of f(n, k) for every 0 ≤ k ≤ n and oeis it, first result will be A130534. Then google Stirling numbers of first kind and get some information from wikipedia about it. Next thing is googling "Stirling numbers of first kind modulo". You will find PDF in second result, look it and there is solution in page 4:
Theorem. For n fixed, the number h(n, p) of Stirling numbers of first kind that are not multiples of p is given by
h(n, p) = (ns + 1)(ns - 1 + 1)... (n1 + 1)h(n0, p)
where (ns, ns - 1, ... n0)p is the p-ary representation of n.
Calculating p-ary representation of number needs O(logp(n)) time, so it is easy to get one part of answer — the multiplication of (ns + 1)(ns - 1 + 1)... (n1 + 1). But, what about h(n0, p)? Notice that n0 < p ≤ 105. And there is one formula in wikipedia:
Can be solved by FFT. Learn FFT, write code and get AC.
By the way, if you are aware of HackerRank Week of Code hard tasks, Stirling numbers of first kind will remind you Sasha and Swaps II problem and you can find FFT code to calculate this numbers in the editorial :)
Ok, so I have a question about FFT. Specifically, numpy's implementation of FFT.
If you (or anyone else) have tried using numpy's FFT (numpy.fft.fft and numpy.fft.ifft), I'd like to know how good it is. At the very least, can it be used in a contest without worrying too much about TLEs and approximation errors?
I came to the answer of the question using FFT, but didn't have time to learn it and implement it myself. Instead, I tried using numpy's version, but that gave me a TLE on even the first subtask. With Python's time limit multiplier, that's 20 seconds — direct multiplication didn't even take a second for the same thing.
So, is the problem the implementation, or is it possibly my use?
For reference, assuming I'm multiplying P and Q, I was pretty much doing:
I hope that's correct?
(I'll try to learn and implement FFT myself soon and figure this out, but I'm just curious in general)
numpy's FFT? Python? It gets AC hardly in C++, I don't think it will pass. But if you know python, why not to check it?
While checking some solutions in python, I noticed that tests of this problem are also very weak, for instance, see this submission: https://www.codechef.com/viewsolution/17348967 . It returned answer is n0 + 1 if n > 40000 and brute-forced otherwise. You can observe that answer is n or n + 1 (mostly n + 1) if n < p, even I have submissions with returning n + 1 for n0 (click). One can find test for n > 40000 and answer for n0 is not n0 + 1. kingofnumbers, please give more attention for tests, some hard problems has really weak test data and it is not good to see one passed tests with wrong solution while you crack your brain on that problem all day.
I don't actually know much Python lol, I just wing it and search what I need to implement whatever I'm thinking of. Python basically comes in when I want to do something with bignums, pretty much everything else is C++.
But yeah, I should probably figure this out myself, you're right.
Is the FFT multiplication right, though? A quick read got me that, so I might be missing something there.
And, that's kinda a shame about the tests...
Very nice FFT tutorial here: http://codeforces.me/blog/entry/43499
It is multiplication of two polynomials in O(nlogn) time instead of simple O(n2).
If you want to use numpy you can also use numpy.polymul, it uses numpy.fft under the hood for bigger multiplications and bruteforce for smaller ones. I also used it and got AC so it's not that slow: https://www.codechef.com/viewsolution/17347833
Can anyone explain, How to solve "BROKEN CLOCK" in simple way. Not able to understand the solutions in submission.
Link for Problem — BROKEN CLOCK
first we calculate all the cos terms of power of two by formula (cos (2*theta) = 2* cos^2(theta) — 1) we have all the cos terms of exponents of 2. Now, while calculating cos terms we parallely compute sin terms also.
Now, the problem is that sin(theta) may be irrational! But this will not affect our answer. Why? : because we are interested in only cos(x) value and we know cos(x+y) = cosx*cosy — sinx*siny. So, as we can see there are two sin terms and both multipled together. and we know while calculating sin(x*theta) we use 2*sin((x/2)*theta)*cos((x/2)*theta). As we further break the sin((x/2)theta) we see that it ultimately stops at sin(theta) (NB : WE ARE ONLY CALCULATING SIN FOR POWER OF 2 SO, IT IS ALWAYS TRUE). so, we can claim that in the above formula the term 'sinx*siny' contains irrational terms in pair(i.e. either both have irrational part(which have same value) or none) so, if we ignore this irrationa part and just compute sin(2*theta) = 2*sin(theta)*cos(theta) then at the time of computing cos(x+y) we simply multiply the whole sin term (i.e. sinx*siny) with (sqrt(l^2 — b^2)*sqrt(l^2 — b^2))!
Now, so far we have all the sin and cos precomputed (all the powers of 2 upto 62). so, how to answer the query(i.e cos(theta)) for a particular 'theta'!
suppose theta = 15 --> 8 + 4 + 2 + 1
we have cos(8*t) and cos(4*t) (and corresponding sin values also) so, we can apply formula cos(x+y) to get cos(12t).
Now, moving forward we have cos(12t) and cos(2t) (and corresponding sin values also) so, again we can get cos(14t).
finally we have cos(14t) and cos(t) (and corresponding sin values also) so, we get cos(15t).!!
Idea is almost same as above comment, calculating cos(n * t) gives us answer. We use cos(n * 2x) = 2 * cos2(n * x) - 1 is t = 2x. But for odd t instead of calculating sine I used that:
We know cos(x) + cos(y) = 2 * cos((x + y) / 2) * cos((x - y) / 2). Replace x = n * t, y = t. So,
cos(n * t) + cos(t) = 2 * cos((n + 1) * t / 2) * cos((n - 1) * t / 2), therefore, cos(n * t) = 2 * cos((n + 1) * t / 2) * cos((n - 1) * t / 2) - cos(t). Use memoization to avoid TLE.
Nice problem.
but how to store values upto 10^18 i came up with the formula cos(n θ)+cos((n-2) θ) = 2cos(θ) * cos((n-1)θ) but where to store values upto 10^18 ?
Your formula will work in O(n) because, if n is odd, you will calculate n-2 which is also odd, then n-4 which is also odd and so on. About storing values, use map.
See my code: https://www.codechef.com/viewsolution/17285268
yes , and since n=t(here) can be large upto 10^18 this was not an effective one as at most everytime i m subtracting 2 from it ... ur formula is divides each θ by 2 therfore it will be much faster.
And pls correct me .. u dont have to deal with irrational values as finally t will be either 1 or 0. am i right ??
Yes. t will be 1 in the end and we know value of cos(x) from input which is not irrational value.
I also got the same formula, but I used matrix exponentiation to solve this equation.
Link to my solution
thats where i got stuck .. didn't have prior knowledge of Mexp. i could store values upto 10^6 but what to do further i was not getting !!
See this for learning matrix exponentiation, just in case you want :)
Here's another idea, perhaps a bit easier to implement. Use the formulas:
cos(a + b) = cos(a)cos(b) - sin(a)sin(b) and
cos(a - b) = cos(a)cos(b) + sin(a)sin(b)
With a = (n - 1) * x and b = x, we have:
cos(n * x) = cos((n - 1) * x)cos(x) - sin((n - 1) * x)sin(x) and
cos((n - 2) * x) = cos((n - 1) * x)cos(x) + sin((n - 1) * x)sin(x)
Add them up and we have:
cos(n * x) + cos((n - 2) * x) = 2cos((n - 1) * x)cos(x), or, equivalently,
cos(n * x) = 2cos((n - 1) * x)cos(x) - cos((n - 2) * x)
This is now a simple linear recurrence, which can be calculated using matrix exponentiation: f(n) = α f(n - 1) + f(n - 2), where α = 2cos(x) and cos(x) = l / d in the input.
See my submission for an implementation.
thats what my above formula is but since n can be 10^18 what u did to avoid tle ?
If you notice, the formula forms a linear recurrence — the one I mentioned at the end: f(n) = α f(n - 1) + f(n - 2), where α = 2cos(x) and cos(x) = l / d.
Essentially, what we need to do is find the n'th term of this recurrence. Again, as you've noticed, doing this directly, even with memoization, is O(n).
However, there is a way to find the n'th term of a linear recurrence in O(logn) by representing the recurrence in the form of a matrix, and then finding the n'th power of that matrix by square exponentiation (the same method you use to find an in O(logn)).
Here's a pretty simple tutorial, which explains the motivation fairly well: http://fusharblog.com/solving-linear-recurrence-for-programming-contest/.
That optimization will let you solve the problem even for very large n — including 1018.
Thank you. Well explained. see lokpati
For explaining convenient, let's rotate the clock 90 degree clockwise. What we need to find now is the x coordinate of the minute hand.
Represent the point P = (x, y) by a complex number C = x + yi. Notice that, when we multiply C by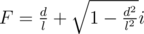 , we rotated the point P by an angle θ around the origin, with
, we rotated the point P by an angle θ around the origin, with 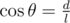 (θ is the angle that the minute hand rotated each second). Why? Because in polar form,
(θ is the angle that the minute hand rotated each second). Why? Because in polar form, 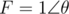 . So, if
. So, if 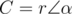 in polar form, then
in polar form, then 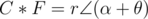 .
.
So, the answer we need to find is the real part of the complex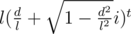 .
.
To calculate this, represent complex number in form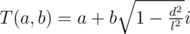 . Then,
. Then, 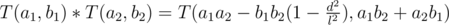 . So, what we need to calculate now is the real part of
. So, what we need to calculate now is the real part of 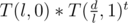 , which can be done by fast exponentiation.
, which can be done by fast exponentiation.
The value for cos(theta) is given. Now we have to find cos(t*theta).
We can do this using chebyshev polynomial of the first kind , since Tn(x) gives cos (n*theta), where x is cos(theta).
The chebyshev equation is: Tn+1(x)=2x*Tn(x)+Tn-1(x).
This can be solved by using matrix exponentiation in O(log(t))
Link to my solution
@sdssudhu in ur solution how you dealt with fractional parts like when cos θ = 4/7 how u handled numerator and denominator seperately & have u caculated modinverse of L in the beginning? if yes , but in the question it was mentioned that after finding the final y coordinate and simplifying it to p/q , then you have to calculate mod inverse of q.
Yeah, for that you can use the matrix property and take the denominator constant out, for example if you have[2a/b,1,-1,0] , then you can have it as 1/b*[2a,b,-b,0]. Now you can multiply the matrix ^ t and then Divide by d^t using inverse modulo. Then you must multiply the answer by l, where l is the length of the clock. See my solution if you want to have a look at the implementation.