We've just rescheduled our contests.
Next Saturday, we'll hold a long (most probably 5 hours, but it is not finalized yet) contest on AtCoder. Note that the start time is unusual: please check here.
The problems are based on one of the problemsets of Petrozavodsk camp. If you are a participant of Petrozavodsk camp, please don't participate in this contest. And of course, please keep the problems secret!
This is a rated contest for everyone, and this contest counts for GP30 scores. If you are a Petrozavodsk participant and you care GP30 scores, please let me know. We'll make sure that you won't get disadvantages (please check here, we'll handle you as a writer, i.e., increase the value of Y by one).
The writers are japan02 team (yosupo, sugim48, sigma425).
Note that AGC 021 was postponed to avoid collision with an Open Cup round.
UPD: the contest is actually 5 hours. contest link
According to http://opencup.ru/index.cgi?data=oci/schedule&menu=index&head=index and https://atcoder.jp/, AGC 021 still collides with an Open Cup round. There's just too many of those :)
I'm sure rng_58 let you rest only for an hour between two 5-hour contests.Sorry, I missed the date of the Atcoder contest. Ignore me.
Yes, then I'll try to move it again. The problem is that there are local tournaments on Saturdays these days...
Sounds exciting!
Hope that this time I will get up sufficiently early >_>
Reminder: The round starts in 1 hour.
How to solve problem F ?
Let d(v) = xor of all neighboring edges of vertex v. Final condition of all value of all edges = 0 is same as saying d(v) = 0 for all v.
Notice that an operation on a path now affects only d(v) values of the start and end nodes.
Pair d(v) values with same mask greedily and for the remaining (at most 16) distinct values, use bitmask dp to compute the minimum number of operations.
Nice trick , thanks)
For every vertex compute xor of its adjacent edges. Note that what one operation is taking two arbitrary vertices and xoring them by the same number. You can also note that if all such numbers are 0 then our current tree has only zero edges, so our problem is reduced to following one:
We are given multiset of nonegative integers not exceeding 15 and one operation is taking two of its elements and xoring them by the same number. What is smallest numbers of operations to make all numbers zero?
We can first greedily pair up equal numbers (don't know why, but got AC :f), so in fact after this our multiset becomes set. Then we can use dp in complexity 3^16 because if we have a set S of numbers of xor==0 then we can solve it in |S|-1 moves and it turns out we just need to find partition of our set into biggest numbers of subsets so that every subset has xor 0. Answer is size of our set minus greatest number of subsets in such partition.
We can even obtain complexity O(Max2·2Max) instead of O(3Max).
If 2 equal numbers are in different groups, then we can merge these groups and take these 2 numbers in their own group.
I find the problem F similar to problem K from CERC 2017.
Well, in my opinion the main observation is the relationship between path XOR and the XOR of numbers on edges coming from vertices. The grouping into subset parts should be relatively standard in comparison.
You are probably right — the reduction from the operation on paths to the operation on pairs in the Petrozavodsk problem is much harder than in the CERC problem than here. (The CERC problem uses a modulo 7 addition instead of XOR, and the graph is — crucially — a path.)
I got that "xor of all neighboring edges" part indirectly without realizing it — not thinking about "for most of the vertices on a path xor remains the same" at any point.
Let's start with rooting our tree and using an observation that doing XOR on a path means the same as doing pair of XOR's on paths starting at the root and ending at the endpoints of original path — part from root to LCP will be common there.
Now it feels like for each vertex we have a value that it need to be XOR'ed with — it is the value on the edge from this vertex to its parent. However, it doesn't take into account the fact that value on this edge is going to be changed after fixing everything in a subtree of the vertex. Luckily since we moved to a problem in which all paths start at the root, we can figure out precisely how these fixes will affect given edge. After thinking on how exactly will this value change (we can assume that all these operations are done before fixing our parent edge since order doesn't really matter) we can discover that the change will be exactly (surprise!) XOR with values of all edges going down from this vertex.
How much code did author wrote for I?
Uploaded the editorial. I is very short.
Wow...
When can we expect solutions to GHJ?
In the worst case in two days, I hope to do it earlier.
What's GHJ?
Problem numbers. Context: The English Editorial for them is not available at the moment.
UPD : It is available now
[shorter version in the first revision]
I'll call "doors" teleports in analogy with the IOI problem Teleporters.
Let's add '1'-s at the beginning and end of S and call this string a topology. Each point i (1 ≤ i ≤ 2N) has an id that's initially equal to i and lies between S[i - 1] and S[i]; if these characters are both '1' or both '0', let's call it a 11-point or 00-point respectively. The remaining points are border points.
Each teleport can only connect two border points (once visited), 11-points (twice visited) or 00-points (unreachable). After connecting some points with teleports, we can try to find an equivalent, shorter topology-string without any teleports; note that each point in this topology needs to keep the same id so that when teleports are added between pairs of points with the same id-s, it gives us the desired solution for the original topology.
Since we can't ever reach 00-points, their locations in the topology are irrelevant; we can simply connect them pairwise and be done with it. This is always possible if there's an even number of these points. If there's an odd number of them, there's no solution, since each such point is one endpoint of an unreachable teleport and the number of their endpoints has to be even (see also: handshaking lemma).
The number of 11-points is now even as well — since S[0] = S[2N] = '1', the number of border points where '1' changes to '0' or '0' to '1' must be even. After connecting pairs of 00-points, we can ignore them and get an equivalent topology without them. Let's first show what to do if the number of 11-points is divisible by 4, since this case is simple.
We can connect each pair of consecutive border points with a teleport. Afterwards, the equivalent topology is obtained by erasing each pair of border points and the corresponding substring '01', and is a single segment of consecutive '1'-s. Since the number of points in it is still divisible by 4, we can take each 4-tuple of consecutive 11-points, connect the 1. to 3. and 2. to 4. with teleports and erase them from the topology. At the end, we're left with the trivial topology "1" and we're done.
Consider now this topology that doesn't contain '0'-s; the number of (11-)points is clearly even (2N), but if it's indivisible by 4, does a solution exist? In other words, if we make a bipartite graph with 4N vertices L1..2N, R1..2N, where Li denotes arriving at point i (from the left) and Ri leaving it (to the right), is it possible to make a Hamiltonian path?
The answer is no, but my proof was wrong. If I find one, I'll post it.
Now, what can we do if the number of 11-points isn't divisible by 4? If we have at most 2 continuous segments of '1'-s (connected to both ends of the topology), there's nothing we can do, because the only way to connect border points gives us equivalent topology to one segment of '1'-s, which has been proven impossible to achieve. Therefore, we need a '1'-segment separated from both ends; if each such segment has length 1 (contains no 11-point), then regardless of how we connect border points, it still gives us topologies without 11-points on segments other than the two on the border, leading to the unachievable topology without border points — we need a '1'-segment containing a 11-point (let's call the first of these points PA and the border points for the segment containing it PE, 1, PE, 2). If no other segment contains a 11-point, then connecting border points leads us to the same unachievable topology again. Therefore, we need a 11-point outside of this segment as well (let's call one of these points PB).
We can now connect PA with PB and PE, 1 with PE, 2. This way, when we get to PB, we'll move to PA, do something that gets us to PE, 2, move to PE, 1, then directly to PA, to PB and continue on from PB. This means we've got an equivalent topology that contains all points between PA and PE, 2 (exclusive, in the same order) instead of PB.
This topology has two less 11-points, so we can use the algorithm for number of 11-points divisible by 4 to find a configuration of teleports that satisfies it.
Uploaded.
It's impressive that the last problem was solved by two people. It wasn't solved in Petrozavodsk (so it will appear in next year's Prime Contest).
I tried to do it for something like half of contest (but failed). This is problem of this kind which seems pretty easy on first glance, but then you discover new cases and after that more of them and after that you discover even more cases etc. :P
+1 :) I think I was quite close actually, but not enough.
I solved it today (link) (during the contest it took me way too long to solve F and then spend the rest of the time on H) and expected there to be lots of cases, but was actually surprised that there were only two.
Either there is a cut in at least one of the dimensions or there is no cut in any of the dimensions. The first case can be handled quite easily with inclusion-exclusion. The second case is somewhat more tricky.
Define a cuboid to be in a pillar if it can be 'pushed down' together with all cuboids 'below' it. If a cuboid is not in a pillar (we need at least one of those, otherwise we would have a cut) then it must be blocked somewhere, either horizontally or vertically or both. Without loss of generality assume it is blocked vertically. This blockage causes the entire vertical slab to be blocked. If this entire vertical slab could be 'pushed down' together we would have a cut, so it must be blocked somewhere horizontally. Continuing in this way we see that all cuboids that are not in pillars form vertical and horizontal slabs that are connected. This also means that all those cuboids are aligned in layers. At least one of the pillars must be shifted relatively to the layers (otherwise we would have a cut) and this shifted pillar causes the rows and columns in different layers to be aligned.
This all means that we need to fill C/c layers so that a given number of the A/a rows (at least one, not all of them) and a given number of the B/b columns (at least one, not all of them) are shifted in at least one of the layers. Each layer is a 2D-version of the problem, were we can either shift some rows, shift some columns or shift nothing at all. This can be calculated with a relatively simple DP and afterwards we can shift the remaining pillars and obtain the answer for the second case.
I hate problems like H. I always think that good authors wouldn't let obvious heuristics pass in one of the hardest problems of the contest. Spent half an hour trying to come up with something provable because of that. Probably would've spent more if it wasn't in the end of contest. I think if the problem costed about 700 points then there would be a lot more OKs.
Well, we didn't know such solutions. What did you do?
We can prove that our intended solution spend O(NlogN) queries (and there's more complicated solution that requires only O(N) queries).
If the tree is a chain, then the following algorithm works: take value in the root, let it be v, start from leaf u and while v is ancestor of au and au is ancestor of u, assign u = pu. Then query u. Let's do the same in the general case. The problem is we don't know which leaf to chose. Obviously, it should be some descendant of v. Let's choose such of them that depth of the vertex that we query will be as great as possible.
I considered that whether this heuristics is correct or the test case is weak, and I think this heristics is good enough to get AC.
The key idea of author's solution is "fill leaf-path-vertices simultaneously"(we define leaf-path-vertices are vertices "that is leaf" or "that have only one child, which is leaf-path-vertices"), and this heuristics seem to contain this idea.
In conclusion, I think this heuristics isn't obvious and have worth to 2000pt.
actually, it is provable. if you connect each node to its deepest child, then you are basically doing hld (the same way dsu works with both size and depth). and if a path has no lighter paths branching off it, then you can just sort it using normal insertion sort. so every n operations, every lightest path gets sorted. and this can only happen log n times, i think
How to solve E?
I'm saddened to say that user FLEA cheated during the contest by using two accounts! Proof: account 1 account 2
PS: sorry if this is not the place to post this but I don't know where else I could do that
He CHEATED and he wrote a LONGER solution!
IT IS NOT A JOKE! To those who do not believe in this. FLEA has got two accounts on atcoder. The first one — grandmixer, is the one on which he participates regularly. Of course he doesn't want to lose points on failed submissions. So he firstly submits the problem solution from the second account — grandfixer, till he gets it Accepted. Then, he happily submits it on the first account. Proof is that the difference in time between the two submissions on different accounts is about 30 seconds, and they look surprisingly identical! To convince yourself, you may check the links above. This is important also for this platform, because FLEA may use the same "trick", here.
how to solve B.I am not able to understand editorial.can someone give me example to illustrate the solution
For indices i with a[i]>b[i], b[i] can be made equal to a[i] by adding (a[i]-b[i]) to b[i]. Thus 2*(a[i]-b[i]) needs to be added to array a[] elements. We distribute 2*(a[i]-b[i]) to some array a[] elements such that no element of array a[] exceeds corresponding array b[] element.
This process is repeated for all indices i with a[i]>b[i] such that finally no a[i]>b[i] remains. If this is not possible, its impossible to make arrays equal. Otherwise we have a arrays a[] and b[] such that for all indices i, a[i]<=b[i]
It can be easily proven that for indices i with a[i]<=b[i], adding 2x to a[i] and x to b[i] can make a[i] equal to b[i].
Time complexity for my solution comes out to be O(n*n) which is enough to pass.
What's testcase 3 and 21 in problem D? I'm getting all AC without these 2! :(
Thank you for participations! I'm suprised that there are 2 person solved J and 17 person solved H(I thought J about 5 hours and got to nothing... ><)
By the way, I like problem I very much, actually this problem's implemention isn't hard, please try by all means.
P.S. writer:(yosupo:BDHI, sugim:CEFG, sigma:AFJ)
Thank you for your participation! I wrote A,F and J. (I made the path version of F, then sugim48 had made the same problem coincidentally! (but that was the tree version, so we adopted this version of course!) I'm surprised that J was solved, because there is no AC in the Petrozavodsk camp. Congrats to ksun48 and tourist, who solved J! :)
Umgh, very helpful thanks! :)
For E, I submitted a solution that did the following:
If the original tree is just a path, then the answer is 1.
Else, root the tree at a vertex with degree at least 3. Then the answer is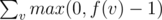
where f(v) is the number of children of v whose subtree is just a path.
Would you please explain why it works? TIA.
This is just a rough outline of the proof:
We get the condition that when we root at any vertex v with degree k we need to choose at least one vertex from the resulting k - 1 subtrees.
The case where the original tree is just a path is obvious.
Now we root the tree at a vertex with degree at least 3. Note that since the root has degree at least 3, from any vertex v there will be at least one vertex chosen that is not in the subtree of v. So thus it is enough to choose at least one vertex from k - 1 subtrees of children of v where k is the number of children of v. Note that obviously all subtrees of children of v that are not simple paths will have at least one vertex chosen under our algorithm, so we don't need to worry about them. So for a given vertex we only need to worry about the subtrees of children of v that are paths. But we can just treat them as single vertices, so we must choose all but one of them. Note that f(v) - 1 = 0 for all vertices that are part of a path, so we won't overcount.
For D,I want to know how to ensure the whole vertices are connected if we choose the vertices from the smallest costs, until we choose 2(N−M−1) vertices in total.Hope any one can tell me the reason,thx a lot!