Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 153 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
| Name |
|---|



I have tried Problem C. First I found all cycles and then I found In how many cycles a edge is present. Then If there is any edge which appear in all the cycles (edgescount==cycles) Then answer is Yes otherwise No.
But I am not able to find all cycles correctly. Can anyone suggest How I can find all cycles in a Directed graph.
Link to my solution http://codeforces.me/contest/915/submission/34176793
You don't need to find all cycles, just one.
If other cycles in this graph share an edge with this cycle you found, then by removing this edge you break the other cycles and make the graph acyclic. If there are cycles which don't share an edge with the cycle you found, then you of course can't make the graph acyclic by removing just a single edge from the graph.
Therefore it suffices to find just one cycle, as the editorial says.
Also I guess that there can be a lot of cycles in a directed graph, maybe too many to store.
I am not storing cycles, I am just Increasing edge count. I think Jhonson algorithm can work.
I did C with simply dfs. I guess it has complexity O(len!), where len is the length of 'a' and '!' is factorial. It passed all the system tests, but I'm not sure that it's correct. 34181569
It seems it's about O(2len).
On each step you either put the digit that is present in this position in b or the greatest digit smaller than it. Like the first possibility lead to the same brute with len - 1 and the other one ends instantly.
Your explanation is't clear for me. I do the cycle from '9' to '0' on each step ( we can consider that we have number = 999.... I can't see there 2^n. Can you explain it more detailed? Maybe on some test. I'm still thinking that it will work for the len 10^3 and more.
You iterate over all digits but only 2 of them will be considered at maximum. It could have been O(10len) instead of O(2len). In worst case you will check bpos with can = false, fail and then proceed to the next present digit (you will get answer in no time).
Thanks, I understood you. But I'm not sure that there is a test with the worst case. On my mind it can fail only once.
I solve it with dfs, too. As a matter of fact, I prefer to considering its complexitiy O(|A|len). 'Cause we have greedy algorithm. First, we choose the maximun digit (also not greater than b1) for a1 and do it again and again. For example, if a1 < b1,we can disgard the limit of not greater than b1, and then whatever remains, we just choose the maximun digit. But if a1 = b1, we just wait until ai < bi.
Does anyone have a faster solution for D? I prefer not to live on the edge.
Need help.
My code for D passed during upsolving. And I have no idea how.
What i did:
Toposort N times (start from a different node every time, still doing a dfs for every connected component, just beginning node is different.)
for each ordering check if the number of edges that fail the relation of toposort is 1 or 0. If any such order exists, then print YES else NO.
Can any one tell me why this worked?? Or maybe the test cases are weak?? I was not expecting this to pass at all. Submission: code //sorry for super poor indent.
Can you give the proof of correctness of this solution?
I tried to find a reasonable explanation but could not get one...this is still a mystery for me..if you have a proof please do share!
Suppose that there is no 1 edge removal solution. Then your code will surely output NO, there is no way to topsort the edges with only 1 back edge.
Next, suppose that there is a 1 edge removal solution, and let that edge be from node a to node b. At one point, your code will do a topological sort from node b. Consider the result of that sort. Surely we shall have the back edge from b to a, but I claim there will be no others. Suppose a,b,c,d are distinct nodes. If there is a back edge from d to c, then there must be a path from c to d as well (because of how topological sort works). But then this cycle does not use the edge a->b at all, so removing the ab edge will leave a cycle, contradicting our earlier claim.
When your code does the topological sort from b, then, it will find a valid solution and print YES. Hence it is correct.
In Problem E, how is the time complexity O(q * logq)? After finding the first interval that intersects with the query, one needs to go over all the following intervals that intersect the query. That should amount to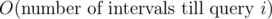 for query i, and hence, O(q2) overall. However, this passes system tests 34180929. What am I missing?
for query i, and hence, O(q2) overall. However, this passes system tests 34180929. What am I missing?
In each query you will add no more than 1 segment (size of set won't exceed q). And those that you touch when updating, you delete immediately, so it's q deletions at maximum.
Can someone explain how t(i) is made in more details?
t(i) is not made explicitly in the program. it is a model that helps you think about the question. What is important is how to determine v_1, v_2, ..., v_k.
UPD : Ok, I understood, but why are we adding every s_i. Let's saz we have root i, its children j and j's children p (this is some part of the tree t(i)) than s_j is 2 and s_p is 1, then we have s_j + s_p choices (based on first summation) which is 3 but we have 2 choices? What am I missing?
So, the idea is that t(i) is the sub-tree that contains the paths and that v_i will be the maxima on all paths of that tree. (otherwise, the given formulae will not hold).
That said, in t(i), v_j is connected to v_i directly if (v_i, v_j) is in the original tree and a_j < a_i. Likewise, v_j is connected to v_i indirectly if (v_j, v_k) is in the original tree and v_k is connected to v_i directly or indirectly.
I understood that and changed question, thank you anyway. Can you help me with new one?
So...let me elaborate your example. Basically, there are 3 paths in your example: The 3 paths are: (v_i), (v_i, v_j), (v_i, v_j, v_p).
However, to get this answer at v_i for the first summation, you will do: s_j + 1 (instead of s_j + s_p + 1).
You will only calculate the sum for neighboring vertices.
So we're looking for s_j of the vertices that are directly connected to i? If yes, everything is clear. Thank you so much
could anyone accept F with centroid ?
I tried...
Can someone explain the segment tree solution to problem E?
Problem E is a simple data structure. What you need to do is to build a Segment Tree. The lenth of it is n(that is, equal to 1e9), but do not build the whole Tree. Only if you want to get some information from the interval, you make it. In a word, that is a dynamic-building Segment Tree.(I don't know what its exact name in English)
I tried implementing this, and it was TLE on test 17. Is there a way to make it faster? Or a special way to implement it?
That's just a simple data structure in my view. Would you mind showing your coding to me?
Thank you! My code is here: 34164827
faced the same.
Try declaring functions as "inline void" instead of just "void" and see the magic.
However, you might have to build the tree a bit more smartly, otherwise memory requirement will be very high.
I have read your code. And my code have a trick that might save time and memory. That's : I count non-working day, and output n - non-working day. At first my Tree is empty, and empty node means its interval is working-day. So if the interval we updated is working-day and we want to it become working-day, we can do nothing. And I suggest you should use scanf/printf instead of cin/cout. 34209709(I pass 17, but RE on 18)
http://codeforces.me/contest/915/submission/34155433 I think my code can help you. I did Discretization
There is no way to get it done with dynamic seg-tree. See, we got values are upto 1e9. Only what is under limit is query Q (3e5). But, for each query there can be node split, so the number of nodes gets too high. For case 18 nodes are higher then 9250000 (max limit of 256MB with 5 ints, 2 pointers and stack). It can be done with discrete segments (by maps) which falls under amortized cost of O(Q log Q).
No, actually you could maintain each node by 4 integers, the left child, the right child, the sum of children, and the lazy flag. So you could allocate about 1.5e7 segment nodes at the beginning of program.See my submission if needed:35567497
Can anyone explain solution for problem E in detail? Thanks!
Problem E is a simple data structure. What you need to do is to build a Segment Tree. The lenth of it is n(that is, equal to 1e9), but do not build the whole Tree. Only if you want to get some information from the interval, you make it. In a word, that is a dynamic-building Segment Tree.(I don't know what its exact name in English)
Author solution is similar with segment tree, but more simple in realization in my view.
Steaunk I saw your solution for problem E but I don't really get it, so can you suggest any resources for this "dynamic-building Segment Tree".
thank you in advance.
I'm sorry. I can't get any English resources (maybe some Chinese articles will be OK). If you really want to know things about dynamic-building Segment Tree(that is, what I called), we can chat or I can write an article (but it'll cost some time).
Yes, if you can it would be useful I hope :)
Interesting thing I have came across just now: we can push all coordinates into vector v and sort them. After that use standart segment tree, replacing ith vertex coordinate with v[i].
Of course, you can sort them. At first I want to use this discretization algorithm, but I think dynamic-building Segment Tree can save time.
You can search "implicit segment tree".
My solution (the same as author's):
0) Let's create set < pair < int, int > > , where we will store all non-working days as {Ri, Li}. The main rule is that segments should not intersect — then we can merge existing segments with new (or cut segment).
ans = n
1) K = 1, we should add segment [L;R] in our set. Let's find all segments where Ri ≥ L (it means that new segment and these can have intersection). We can find first such segment by lowerbound({L;0}) (remember that set sorted by Ri). While Li ≤ R we should continue iterating over set, on each iterate we are merging segments:
-make L = min(L, Li), R = max(R, Ri)
-erase segment {Ri, Li} from set — now it is contained in our [L;R] segment.
-ans = ans + (Ri - Li + 1) — formally we erased segment and made days [Li;Ri] working (but we will change it later).
When we archieved Li > R or end of the set, we make:
-insert our merged segment {R, L} in set
-ans = ans - (R - L + 1)
-print ans
Example: we had set = ({1, 1}, {5, 2}, {10, 7}, {13, 12}) adding segment with L = 4, R = 9
lowerbound({4, 0}) will find us first pair {5, 2}, 2 ≤ 9:
L = min(4, 2) = 2, R = max(9, 5) = 9
then pair {10, 7}, 7 ≤ 9:
L = min(2, 7) = 2, R = max(9, 10) = 10
then pair {13, 12}, 12 > 10, stopping and inserting resulting segment {2, 10}.
resulting set = ({1, 1}, {10, 2}, {13, 12})
2) K = 2, similar with previous one, but we are cutting stored segments (and insert them back at once) and do not insert something at the end.
Can you explain the total time complexity for this ?
We get q queries. Suppose we have q - 1 pairs in our set before the last, qth step.
If K = 1, on each iteration we are merging two segments and after x iterations we will have q - 1 - x segments in set. It will take us q log q operations (q segments * set complexity).
If K = 2, on each iteration we are deleting or spliting segment and after x iterations we will have about q - 1 - x segments in set too. Remember that we can split only two segments at most on each iteration (which are insersecting our [L;R] segment) — another are contained in [L;R] and we are erasing them. The same complexity.
Another explanation: think about maximum operations for one segment in average. As we merged ith and jth segment, it becomes jth. And as we merged jth and kth segment, it becomes kth. And as...
O(q log q)
What is the datastructure that keeps elements in the set sorted and supports deletion operation
set is based on black-red (autobalanced) tree as I remember. That's why it has log2(N) complexity.
You can read articles about binary-search trees in articles, like this: https://www.geeksforgeeks.org/binary-search-tree-set-1-search-and-insertion/
Pictures helps to understand the main idea very much.
Has anyone solved Problem D using approach which is given in editorial by first finding one cycle
http://codeforces.me/contest/915/submission/34172029
How to solve E using segment tree?
The idea is the following. We simply create an array of size n. array[i] = 1, if i is a working day, and array[i] if not. For each query L R k I update all elements between array[L] and array[R]. The sum of all elements is the answer.
But doing a range assignment / computing the sum takes O(n) time. Way too slow.
Since this are range assignments and range sums, the solution is obvious: lazy segment tree. This will give O(log n) per operations. Much better.
But a lazy segment tree will take O(n) memory. That is too much, since n is really big.
There are two approaches to fix this.
1) The first one is to compress the indices. (This means, if there are only the three queries 1 100 1, 50 150 1, 20 80 2, then the elements 1, 2, ..., 49 don't actually need to be represented by 49 single nodes. We can combine them, since they always have the same value. Similar with the other intervals. I.e. we can create an compressed array that represents the segments [1-19], [20-49], [50-80], [81-100], [101-150]. The first element will switch between 19 and 0 (depending it all elements in that interval are working days or not), the second one between 30 and 0, ... depending if the complete segment consists of working days or not.
2) The second approach is to make a dynamic segment tree. The idea is this: since q is not really big, we will only visit a small part of the tree. Most nodes in the segment tree will never be visited. So we can save quite a bit of memory (and time), if we only create the segments that we really need. We start with only one node [1-1e9]. If we need to go to the children, we simply create them on the fly. I.e. if we want to visit them, we simply create two nodes [1 — 5e8] and [5e8+1 — 1e9]. And if we have to go deeper on the left side, then we create more nodes there. Since one range query only visits O(log n) nodes, we have a total memory and time complexity of O(q * log n). In the implementation each segment will have to pointers pointing to the left and the right child, and which are possible null.
You can check out my implementation: 34199755
I have a doubt in your first approach..
What if the right index of one query is same as left index of another one.
Example:
2
1 50 1
50 100 1
What would be the segments in this case?
In this you would need three segments [1-49], [50-50], and [51-100]. So at first the compressed array is [49, 1, 50] (each day is a working day), then after the first query the array would be [0, 0, 50], and after the second query [0, 0, 0].
It's quite tricky to get the segments correct. That's the reason why I implemented the second approach. :P
Thanks!!! Understood it now.
Is it ok to use so many pointers? I remember I tried to solve one task with Decart tree on pointers and got runtime error in case of exceed dynamic memory.
I got accepted. So yes, it is ok. But it was really close. If n or q would be a bit higher, then the solution will get MLE or TLE.
A better approach is obviously the one of the official editorial. O(q log q) instead of O(q log n).
I am trying to do it with dynamic segment tree , but getting MLE on testcase 6, Can you suggest some optimizations.... Here is my implementation Thanks..
Maybe remove start and end variables from the the struct. Also use ints instead of long long.
Also you can try to use a vector/array of fixed size to store the structs (see my solution) but I'm not sure if that will help or not.
Thanks for the reply .. I got rid of MLE , by doing as you said but getting TLE on test case 17. What I have not done is the part , to create vector/array of fixed size. I would like to know, does creating whole array initially , optimizes the code? and How will I be sure that it will not need more space? Implementation that gives TLE
I had the same problem. Creating it with a vector is faster. But I cannot explain why.
I got TLE on test 17 using implicit segment tree, i've seen your code and what's different is that you reserve some memory at first while i using the new constructor c++. Is that really that fast when you reserve some memory at first?
Code : http://codeforces.me/contest/915/submission/34274147
I also cannot explain it. But it worked for me. (I also had to switch after seeing the approach in a different solution).
I used coordinate compression with normal segment tree with lazy propagation. Very easy solution. https://codeforces.me/contest/915/submission/83613121
How can I make this solution to pass? It applies the same idea as described in the editorial: 34202909
Can someone please explain F and G in more detail?
Explanation for F Explanation for G
Edit:updated problem f link
In problem E, can someone tell what optimizations I can make? http://codeforces.me/contest/915/submission/34222959
I did the same as the editorial explained.
Try to use scanf/printf mine solution too passed by using them.
yeah got AC thanks
I notice that there's a "flows" tag in 915G (Problem G). Can anyone explain how this problem can be down using flows?
Same here, I thought flow's best case runs in O(n^1.5) time (biparite graphs), even if a solution exists how come it can fit into the TL?
how to do question 915C using bfs? Can somebody explain!!
I wonder how to find divisors for every numbers in [1,k].
I use a preprocessing to find every multiple for numbers in [1,k],which is O(k log k),and store the divisors in std::vector but got a MLE.
At last I have to set a constant S=5e5 and find divisors with O(sqrt(i)) brute force when i<=S,and store the divisors when i>S.It got Ac,but it's really strange.The editorial didn't mention the way to find divisors,so how can we deal with MLE?
In problem D, I assumed if we destroy a node from this graph and can not find a cycle then the desired edge should be connected with that node(from and to). I took one node that meets that condition. So, now It is just needed to destroy at most (n+n) edges. So, total complexity is O(n(n+m)).
But the assumption is wrong, any node that meets that condition does not necessarily have the desired edge connected with it. So, I took all nodes that meet that condition and checked randomly from each node till I get a desired edge. This one passed in less than half second. Total complexity is O(k*n*(n+m)) where k is number of such possible node. But I think in practical this k should be very small. I can not come up with any graph to disprove this and I am not also sure if the k should always be very small.
.
I think there is a mistake in problem c's statement
first it says "not exceeding b" then it says "not greater than b" :\
I hope you fix it.
Both phrases have same meaning.
if so I'm sorry.
I thought the first means (a < b) and the second means(a <= b)
It's okay.
In problem G: we can prove that the number of arrays with gcd = 1 is the sum of the following values over all possible sets S ...
Can someone please provide some hint or link to the proof?
KEK
LOL
I solved problem C by using greedy. It's quite hard for me to implement this solution. But I am training DP, and this problem was tag
DP. Could you give me hint to solve this problem using DP or It is just wrong tag.Problem D can be solved in O(n + m). Let's build SCC (strong connectivity components). Now let's notice that if we have more than 1 SCC, then the answer is NO. Otherwise, if our SCC has the number of edges equal to the number of vertices, then the answer is YES (sorry, there is not full idea)
I solved C using recursion, the idea is same as the editorial. Submission
I have some problems about E. I implemented a dynamic segment tree with pointers and got TLE、MLE. So I use fake pointers instead of pointers, however it got WA. Then I changed some details (I let
auto &a = seg[id]and operate onain the second version. I changed all theatoseg[id]in the third version.) and got AC.I'm very curious about why my second version of code got WA. Can anyone tell me why.
Here are my three submissions : 244770506 244771884 244772256
Sorry for my poor English and I really appreciate your help.