radoslav11's blog

Can someone hack my G?
By radoslav11, history, 7 years ago, In English

Hello,

During the last educational round I had a solution with treaps for which I cannot construct a sample to make it TLE. It seems to me that the solution is 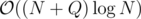or something like that but I cannot prove it. So can someone either provide a counter sample or help me prove it. Thanks in advance!

Here is a link to the submission.

  • Vote: I like it
  • +63
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

I think it should pass. Worst case happens when you are doing query in sequences like this — "12121212..121", and changing 1's to 2's. I mean too many intersections. But once you change all 1's to 2's, then next time there will be a large range of 2's, which is good. And if you transform 1 to something else then that will be just , as the while loop will run only once.

So, I think the while loop runs O(n) over all queries. So it is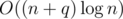 overall.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    I don't think you can simply say that this is the worst case... Obviously many intersections is bad, but in the case when you have just 1's and 2's the problem becomes much easier — just store intervals of consecutive equal values, because changing 1 to 2 on some interval is the same as setting everything to 2. This is not true in the general case though.

    If you take the case when you have lots of intersections, but there are many different values, I don't think you can analyze it this easily — you could try to look at each pair of values separately, but then you would get a big constant like A or A2 (where A is the number of different values) in the complexity. I'm also unable to prove it but I think the complexity of this approach is subquadratic independent of A (so it solves a more general problem).

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

https://www.hackerearth.com/practice/data-structures/advanced-data-structures/segment-trees/practice-problems/algorithm/replace-27c5286c/ . This is a harder version of problem G. Also the editorial explains the complexity. My implementation http://codeforces.me/contest/911/submission/33747581 .

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    As far as I read, the editorial didn't actually explain the complexity of their solution. It uses a different approach (persistent segment trees instead of treaps) but in general has the same idea / problem: efficiently merging two nonempty nodes from the two different trees. Their approach is to call merge two times recursively — separately on the two left and the two right children of our nodes.

    The editorial says that this algorithm had complexity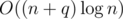 but it doesn't explain why splitting the recursion doesn't impact overall complexity.

    To me it seems like the number of splits the recursion does would depend on n. If that were the case, the complexity would have to be something greater than .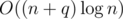

    → Reply
»
7 years ago, # |
  Vote: I like it +44 Vote: I do not like it

You can prove an amortized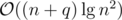 bound.

For a BST A = (a1, ..., ak) define the potential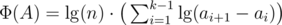 . The total potential is just the sum of Φ over all trees.

If you split A between aj and aj + 1, you loose the term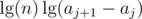 , the potential doesn't increase, hence the amortized time is .

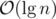If you concatenate two trees A, B (your 'merge' function), you get an additional term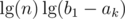 which is at most 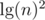, so the amortized time is .

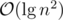When merging two trees A, B (your 'while(mid)' loop), the resulting tree's in-order will consist of blocks contains only as or only bs. The number of loop iterations is linear in the number of blocks. (I think it's around half the number of blocks.) Let's look at a non-boundary block of b's.

and the potential

(We get the as every block boundary is considered in an a block and a b block.)

Note that bj < bl, so

by Jensen's inequality for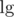 . Hence the potential decreases by at least 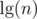for every non-boundary block. This amortizes the 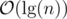-worst case time of stuff we do inside the loop. The boundary blocks increase the potential by at most 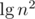, so the amortized runtime is .

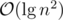Since the sum in Φ(A) contains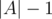 term which all are 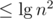, the initial potential is at most 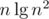. Hence the total runtime is amortized .

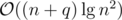I think you can get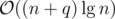 by using finger search trees.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +5 Vote: I do not like it

    I may have misunderstood something, but not every block boundary is considered in both an a and a b block.

    Let's say that we're merging two trees A = (0, 8) and B = (4). Let's denote the tree we get after the merge with C = (0, 4, 8).

    Before the merge we have Φ (A) = lg(n)·lg(8 - 0) = lg(n)·lg(8) = 3·lg(n) and Φ(B) = 0. The total potential is Φ1 = 3·lg(n). After the merge we have Φ(C) = lg(n)·(lg(4 - 0) + lg(8 - 4)) = lg(n)·(lg(4) + lg(4)) = lg(n)·(2 + 2) = 4·lg(n) .

    The total potential didn't decrease by lg(n) — it even increased.

    Also, what's the purpose of the lg(n) term before the sum? I mean, doesn't it always stay there, so it's basically a constant ?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +5 Vote: I do not like it

      The first and last block boundaries are the ones that are not considered twice. Their contribution is at most .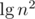

      We need the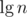 factor to amortize the 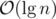time (from BBST split/concat operations) of a single loop iteration, as the 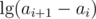parts only give us a decrease of 1 per iteration.

      PS: You can type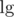 \lg to get nicer .

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 3   Vote: I like it 0 Vote: I do not like it

        My bad, I didn't see that you had addressed my concern a few sentences later. So your proof seems to be correct.

        I meant that you can define your potential as Φ(A) = lg(a2 - a1) + lg(a3 - a2) + ... + lg(ak - ak - 1). Then it will be an upper bound of the number of merges the while(mid) loop does, each requiring O(lg(n)). Again you will get an overall complexity of O(n·lg(n) + q·lg2(n)).

        And I was aware of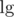 but while "nicer", it displays as an image and not as text. When

        Unable to parse markup [type=CF_TEX]

        is rendered as an image it sometimes doesn't display when I click "preview" (at least in my browser). I didn't want to use an external

        Unable to parse markup [type=CF_TEX]

        editor, so i stuck to just using lg().
        → Reply