Hi, I was solving a problem and it required printing euler path on a directed graph Now,I was unaware of the how to do euler path finding on a directed graph, I tried to search on google but no luck..
What exactly are the conditions that are to be fulfilled to KNOW that a euler path exists and also what are ways to print it... I know of "Fleury’s Algorithm" , but as far as I know (and I know little), this algo is for directed graphs only.. Also came to knew about " Hierholzer’s Algorithm" but this also seems to be working on undirected graphs..
The problem that I was attempting -- 508D - Tanya and Password
The editorial of this problem mentions some points regarding finding euler path on directed graphs but it's not very clear and provides no explanation...
Please can some one help me and also possibly provide me with resources where I can study this?!
Have a nice day!











For directed graphs the condition is that all vertices are in one strongly connected component (you can reach every vertex from every other) and the in-degree must be euqal to the out-degree for every vertex.
Hi, Sorry but I went to this site to look for help earlier before asking this question, website
Here it says that the 2 conditions you mentioned are requirement for a Euler Cycle.. In the problem i was attempting , there is only a requirement of Euler path and not cycle in directed graph,please clear my misunderstanding..
Eulerian Path criterion is the same, except two vertices v, w such that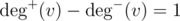 and
and 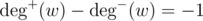
Also
More precisely, all non-isolated vertices
I am sorry , I didnt get the exact conditions!.. I get that it is ALLOWED to have at most one vertex with in_deg — out_deg = 1
and it's also ALLOWED to at most one vertex with out_deg — in_deg = 1
all other vertices must have in_deg == out_deg,
but , The last condition "all non isolated vertices must be in a SCC" feels like it's a necessary thing to have if we want Euler cycle, it seems to me that it's not very necessary for a Euler path...
This graph for example ..
1 --> 2 --> 3 --> 4
does not have all the vertices in one SCC but is obviouly a Euler path..
Digraph must have both 1 and (-1) vertices (Eulerian Path) or none of them (Eulerian Cycle).
Last condition can be reduced to "all non-isolated vertices belong to a single weakly connected component" (see yeputons' comment below).
Thanks! and what you pointed out about (1) and (-1) is GREAT , and obviously true because of SUM(in_degree) = SUM(out_degree) in graph,
Thanks for the help :)
Can you provide some resources to know more,from where do these conditions come from , perhaps a proof , or some readings, where did you study this from etc.
Eulerianity criteria are given in Competitive Programmer's Handbook (without proof) as well as an algorithm to find eulerian path/cycle.
Thanks a lot!!
I believe there is a simpler constraint: if one removes "directness" of edges, then the graph without isolated vertexes should be connected.
yeputons, This feels right and is consistent with examples I could come up with.. So you came up with this through intuition or are there any resources I could read up to understand this , there is a lot of confusion regarding this in my head,..
Thanks for the tip tho , it seems to work!
Well, the proof I know simply doesn't require strong connectivity. It goes like this: let's take an arbitrary vertex v and start building a cycle from it, on each iteration we go through an edge which we haven't visited yet. At some point, we're unable to do so. Note that it can happen only if we're standing in the vertex v, otherwise the vertex would different number of incoming/outgoing edges. So, we have a cycle. Now pick up another vertex, etc, until all edges of the graph are visited.
So we ended up with several cycles which cover all edges of the graph exactly once. Note that if we have cycle C1 and C2 which have at least one vertex x in common, we can merge these two cycles into one. Now, as the graph is weakly connected, we can merge all of our cycles together.
should'nt we start from the one vertex with out_degree = in_degree + 1 (if there is one , if not start from any) .. either this vertex gives the Euler path or NO vertex can give euler path
That's right if we're looking for an Euler path, not Euler tour.
What's for this case? 3 1 1 2
Here it opposes connectivity. So, no eulerian path and Cycle right?
That is for Euler circuit. Can you please tell the condition for Euler path in directed graph?
Check my submission 77697447, it's a solution the problem referenced above. I've also added a comment for the condition of existence of an Euler path in a directed graph, along with the book reference.
Does Fleury's algorithms work in directed graph if we consider the underlying undirected graph while finding bridge?
Yes , Fluery's algorithm works on both directed and undirected graphs, and yes we do consider given edges as undirected when finding bridge.
Simplified Condition : A graph has an Euler circuit if and only if the degree of every vertex is even.
A graph has an Euler path if and only if there are at most two vertices with odd degree.
Your criterion works only for undirected graphs.