tantam75's blog

Question about an array's problem
By tantam75, history, 7 years ago, In English

(Sorry for my bad english!!)

Problem (QBSEGPAR — Vietnam Olympiad of Informatics 2005): For an integer array a1, a2, ..., an and a integer k. Determine the smallest integer M to divide the array into k non-empty parts so that the sum of the elements in each parts does not exceed M.

  • Constraints: k ≤ n ≤ 15000, |ai| ≤ 30000.

UPD: For example, we have n = 5, k = 3, and the array is 4, 3, 2, 1, 5. Then here is one way to divide the array into 3 parts: [4, 3], [2], [1, 5]. You can also represent one way to divide the array into k parts by an array x1, x2, ..., xk (1 ≤ x1 < x2 < ... < xk = n) which part ith (i > 1) is subarray [xi - 1 + 1..xi] (first part is subarray [1..x1]).

I have an 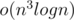solution, which we do binary seaching for M, and dp to check if this M could satisfy (let f(i, j) = true means you could divide array a[1..i] into j parts so that the sum of the elements in each of j parts does not exceed M. Otherwise, f(i, j) = false. Then we can divide array a[1..n] into k satisfied parts if f(n, k) = true). Of course this couldn't pass all tests.

Then I checked for the solution. Here is it, we also do binary searching for M, but for each M, we do a different dp:

  • fi = minimum number of parts which has sum of elements does not exceed M that you could divide from array a[1..i].
  • gi = maximum number of parts which has sum of elements does not exceed M that you could divide from array a[1..i].

Required complexity is o(nlogn2). We can calculate f and g by o(nlogn) dp, which need segment tree or Fenwick tree (i haven't done it), or simple o(n2) dp. Okay, now here is the checking part, which is unclear to me: The solution said that array a[1..n] could divide into k satisfied parts if fn ≤ k ≤ gn. I think this might not be right. In my opinion, we can divide array a[1..n] into minimum fn satisfied parts, maximum gn satisfied parts, but it doesn't mean we can divide the array into k satisfied parts which fn ≤ k ≤ gn.

Could you tell me how to prove this solution right or wrong? Thanks for your help!

  • Vote: I like it
  • +19
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

There was a mistake in complexity. Complexity of binary searching should be log(n * 30000) because my search range was [ - 30000 × n, 30000 × n] (I was so lazy to search for more efficent range).

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

divide the array into k non-empty paths

What do you mean by a path? A subarray?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I'm 99 percent sure that's what he meant by a path (given that the solutions he discusses would make sense that way and that the subsequence variant doesn't seem solvable, at least not this easily, in polynomial time)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      If "part" is a non-contiguous subarray, then this is Minimum makespan scheduling, which is NP-hard.

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 6   Vote: I like it 0 Vote: I do not like it

    Yes, paths are subarrays, sorry for not include that. For example, we have n = 5, k = 3, and the array is 4, 3, 2, 1, 5. Then here is one way to divide: [4, 3], [2], [1, 5]. You can also represent one way to divide the array into k paths by an array x1, x2, ..., xk (1 ≤ x1 < x2 < ... < xk = n) which path ith (i > 21) is subarray [xi - 1 + 1..xi] (first path is subarray [1..x1]).

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    My mistake, i was using wrong word. 'parts', not 'paths'.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by tantam75 (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Let P = {[1 = i0, i1], [i1 + 1, i2], ... [ifn - 1 + 1, ifn = n]} be a partition into fn parts; and let Q = {[1 = j0, j1], [j1 + 1, j2], ... [jgn - 1 + 1, jgn = n]} be a partition into gn parts.

If fn = gn, then there is nothing to prove, and if fn < gn, then by the pigeonhole principle, at least two of the js lie in the same element of P. But note that any such pair must be continuous, so the situation is that for some p and q, ip + 1 ≤ jq < jq + 1 ≤ ip + 1, so we can modify P into a partition with fn + 1 elements. Clearly we can keep repeating this until we reach k elements, so we're done.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I don't get how you split to get fn+1 elements.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Keep all parts the same, except split [ip + 1, ip + 1] into [ip + 1, jq] and [jq + 1, ip + 1].

      EDIT: Nevermind, this doesn't work.

      → Reply