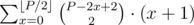hi how to solve the problem change from the spoj (http://www.spoj.com/problems/TPC07/)
i read concrete mathematics chapter 7 about coin change. but i can't able to understand can anybody help me to get idea about solving this problem ?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 4 | atcoder_official | 158 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
hi how to solve the problem change from the spoj (http://www.spoj.com/problems/TPC07/)
i read concrete mathematics chapter 7 about coin change. but i can't able to understand can anybody help me to get idea about solving this problem ?
| Name |
|---|



This is a dynamic programming problem. First learn something about it, then approach this problem
The upper limit of n is quite large, where 1 ≤ n ≤ 1000000000. How to cater for this with DP?
Probably there is a more general formula?
Well the idea is for dp, but you need to use matrices to run it fast, in time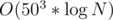 (50 is the maximal value of a coin).
(50 is the maximal value of a coin).
I can explain more if you want.
It can be solved in O(1).
We want to count the number of solutions of x1 + 5x2 + 10x3 + 25x4 + 50x5 = N.
x1 must be congruent with n%5, so is equivalent to count the number of solutions of x1 + x2 + 2x3 + 5x4 + 10x5 = ⌊ N / 5⌋ = M
Let's suppose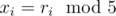 (i.e xi = 5ai + ri), for i ≤ 3.
(i.e xi = 5ai + ri), for i ≤ 3.
We can brute force all possibilities of ri, now we have to count the solutions of
a1 + a2 + 2a3 + x4 + 2x5 = ⌊ (M - r1 - r2 - 2r3) / 5⌋ = P
Grouping, (a1 + a2 + x4) + 2(a3 + x5) = P which can be solved by