Starts in around 38 hours.
Thanks to square1001 for telling me about it.
https://www.timeanddate.com/worldclock/fixedtime.html?msg=SRM%20726&iso=20171219T1600&ah=2&am=0
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3898 |
| 2 | tourist | 3840 |
| 3 | orzdevinwang | 3706 |
| 4 | ksun48 | 3691 |
| 5 | jqdai0815 | 3682 |
| 6 | ecnerwala | 3525 |
| 7 | gamegame | 3477 |
| 8 | Benq | 3468 |
| 9 | Ormlis | 3381 |
| 10 | maroonrk | 3379 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | Dominater069 | 160 |
| 3 | Um_nik | 160 |
| 5 | atcoder_official | 159 |
| 6 | djm03178 | 157 |
| 7 | adamant | 153 |
| 8 | luogu_official | 150 |
| 9 | awoo | 149 |
| 10 | TheScrasse | 146 |
Starts in around 38 hours.
Thanks to square1001 for telling me about it.
https://www.timeanddate.com/worldclock/fixedtime.html?msg=SRM%20726&iso=20171219T1600&ah=2&am=0
| Name |
|---|



It collides with the coming Codeforces 453. :(
Reminder: The contest starts in 4.2 hours. Registeration starts soon.
UPD: Registeration has started! Let's participate and enjoy!
How to solve Div1 500?
One important idea of this problem is to use "centroid" of tree.
If you have centroid c, you have some subtree which connects to c, and let the size s1, s2, ..., sk. Now you have 2sk ≤ n.
First, visit vertex c. Then, visit any vertex (I don't have a proof, but I selected farthest vertex among which I can choose) of which si is maximum among subtree i is not most recently visited. Then decrement si.
I did this thinking and got passed. Anyway, it was an interesting problem :)
With this approach centroid does get maximum possible number of visits but what about other vertices?
For Div2 1000, my recurrence was:
dp(i, j) = dp(i - 1, j) + (j&2k) * dp(i - 1, j XOR 2k) for k in [starti..finishi].
This wasn't working on samples — what's the correct recurrence?
Someone please help with the solution of Div 2 1000?
The problem with the recurrence is that it double counts some configurations, i.e, you'll fail in a case where s = [1], f = [10] (the answer is 2, but I believe this dp will give you something like 11 or something).
To solve this, it requires some observations. First, given a set of intervals, how do you determine if Hero can do them all?
You can do the following greedy algorithm: Sort all the endpoints by finish time (breaking ties arbitrarily). Then, for each interval in order, assign it the earliest available time. The proof is by exchange argument, you can try yourself.
Now, you can apply this idea to a dp approach to count. First, sort all the intervals in order by finish time and add them in one by one. Then, your dp transition is very similar, but you need to break your loop once you find something where j&2k! = 0. The reason you break is that you are basically simulating the greedy algorithm above. There are some solutions in the practice room if you'd like to look at an implementation.
I Think there are 3 cases for div 1 250,
Min cost to make a[i] + b[i] ≥ 2 * k - 1,
Min cost to make a[i] - 1 ≥ K
Min Cost to make b[i] - 1 ≥ K.
I realized this too late but this is the intended solution right ? This passed in practice for me.
unrated again?
It's rated without ANY issue, and my rating changed from 2083 to 2143. Also, you can check rating change of all contestants from https://community.topcoder.com/stat?c=round_stats&rd=17048&dn=1 .
it has a QUESTION mark in the end. it is a question.
How to solve div1 1000?
I have a solution with time complexity O(m3) where m = max (finish[i]) but I don't know how to improve it. Can anyone help me?
You need to sort the queries by cost and run Kuhn's algorithm. One part of the graph is queries, it's very big, the other one is points in time, it has only X = 2000 vertices. Store all unused points in time in set. When you run dfs, you need to find any unused point on a segment, you can do it with lower_bound. This way, each run of dfs will work in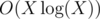 , so overall complexity will be
, so overall complexity will be 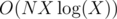 , which is still bad. To fix that, only clear used vertices when you actually find augmenting path. This way all runs of dfs together until we increase the matching will take
, which is still bad. To fix that, only clear used vertices when you actually find augmenting path. This way all runs of dfs together until we increase the matching will take 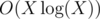 time and we increase the matching only O(X) time so complexity will be
time and we increase the matching only O(X) time so complexity will be 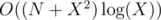 .
.
Alternative solution (solution in practice room — I had a small bug in the contest):
A test of tasks can be assigned to days if and only if, for every time interval [L, R), at most R-L tasks are chosen that fit entirely within that interval. Now work through tasks in decreasing order of cost and try to add each, checking the condition each time.
Naively that's O(m3n), but it can be sped up. Firstly, for each L, keep track of the largest R such that the interval [L, R) has zero slack; call this S. Let T[i] = min{S[j] | 0 <= j <= i}. Then a new task [a, b) can be added iff b > T[a]. We can update S and then T after each new task is added, which allows tasks to be rejected in O(1).
We still need to be update to update S efficiently. For each [L, R), let XLR be the slack in the interval [L, R). For each L, maintain a segment tree with all XLR. The segment tree needs to be able to support range addition, and a query of the minimum value and the rightmost position of that minimum value (in fact the global minimum will always be zero since XLL = 0, but phrasing it this way makes it practical to implement as a segment tree).
This gives run-time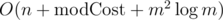 , assuming a bucket sort for the costs.
, assuming a bucket sort for the costs.