Problem: Maximal Average on Array

→ Обратите внимание

До соревнования
Rayan Programming Contest 2024 - Selection (Codeforces Round 989, Div. 1 + Div. 2)
07:08:12
Зарегистрироваться »

*есть доп. регистрация

До соревнования
2024-2025 ICPC Asia Jakarta Regional Contest (Unrated, Online Mirror, ICPC Rules, Teams Preferred)
21:38:14
Зарегистрироваться »

→ Лидеры (рейтинг)

№	Пользователь	Рейтинг
1	tourist	3993
2	jiangly	3743
3	orzdevinwang	3707
4	Radewoosh	3627
5	jqdai0815	3620
6	Benq	3564
7	Kevin114514	3443
8	ksun48	3434
9	Rewinding	3397
10	Um_nik	3396

Страны | Города | Организации

Всё →

→ Лидеры (вклад)

№	Пользователь	Вклад
1	cry	167
2	Um_nik	163
3	atcoder_official	162
3	maomao90	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	155
8	TheScrasse	154
9	Dominater069	153
10	djm03178	152

Всё →

→ Найти пользователя

→ Прямой эфир

Детальнее →

Блог пользователя Hoyda

Problem: Maximal Average on Array

Автор Hoyda, история, 7 лет назад, По-английски

Problem: You are given an aray of N elements(N<1e6). You have to find maximal average of some continuous part of array. Minumum length of part=A, Maximum length =B (A,B<N).

Example: A=2,B=4,array={1,-3,6,2,5} Answer: 4.333

How to solve this problem?

zor, average

Hoyda
7 лет назад
16

Комментарии (16)

Написать комментарий?

khadaev

7 лет назад, # |

+30

Use binary search on answer. We want to know if the answer is more than x. Subtract x from all elements. Now we want to find a segment with length from A to B and a positive sum. Can you do it?

→ Ответить

Azuz

7 лет назад, # ^ |

Actually, it took me a moment thinking about what you said this is a good idea for the check method in the binary search. If I got it right when you find a segment of length From A to B with positive-sum this means that we can obtain a better answer.

Also, khadaev do you think we can optimize the part where we look for the segment of length from A to B using prefix sum (calculated once in the beginning)? Or do you have any idea about it?

→ Ответить

khadaev

7 лет назад, # ^ |

We need to find max(p_i + a, ..., p_i + b) for all i where p_i are prefix sums. Easy way: use segment tree. Faster way: use queue with a maximum.

→ Ответить

Azuz

7 лет назад, # ^ |

great, thank you :D

→ Ответить

satyaki3794

7 лет назад, # |

Binary search on answer. You will need to check if average of any subarray >= A. Then just subtract A from each value of the array and the problem reduces to — check if sum of any subarray >= 0. That can be done using DP. Time complexity is O(N*logA). There might be better solutions than this one.

→ Ответить

ABalobanov

7 лет назад, # |

Run a binary search for an answer. So, now the problem is how to check is there a subarray of a length from that interval with average no less than x. Using the array of the partial sums s_i = a₁ + a₂ + ... + a_i, s₀ = 0, average of interval (l, r) is equal to $\text{[math]}$ . So you have to check is there a pair 0 ≤ l < r ≤ n such that $\text{[math]}$ . Then s_r - s_l ≥ x * (r - l). s_r - x * r ≥ s_l - x * l. Denote t_i = s_i - x * i, then our condition turns to t_r ≥ t_l. Iterate through r and then you need to check is there a l: r - B ≤ l ≤ r - A that t_l ≤ t_r. So you have to take the minimum from the segment (r - B, r - A) from the array t. It can be done with the segment tree(not sure it will pass the time limit) or you can use the special queue which allows to add and remove elements and to take a maximum. Last one will work in O(n * log(ANS * eps))

→ Ответить

Hoyda

7 лет назад, # |

Thanks. After thinking about using binary search its not hard. Checking can be done with multiset in O(nlog n).

→ Ответить

jcg

7 лет назад, # |

← Rev. 2 →

Binary search in the answer isn't needed. Consider taking partial sums s_i = a₁ + ... + a_i, with s₀ = 0. Then the average of segment (i, j] is equal to $\text{[math]}$ . Look now for every index i the point p_i = (i, s_i). Now the average of a segment [i, j) is the slope of points p_i and p_j, if we fix the right point j, we need to look for the point p_i with A ≤ j - i ≤ B that maximize the slope with p_j. Isn't difficult to prove that this point will be in the lower hull of the candidates points. Plus if we look the slopes with the points in the lower hull, the slope first increase and then decrease so we can do a binary search for find the optimal point. This give us an $\text{[math]}$ solution, without doing binary search on doubles!!!. And I think (I'm not quite sure now) that it can be improved to an O(n) since we only need the global optimum.

→ Ответить

ko_osaga

7 лет назад, # ^ |

How do you find a lower hull on interval [i-B, i-A]? you should insert and delete points in CH

→ Ответить

jcg

7 лет назад, # ^ |

← Rev. 2 →

The point are added in increasing x coordinate, so we can update the lower hull in O(1) amortized, using a variant of Andres's Scan (page.mi.fu-berlin.de/panos/cg13/l02.pdf). When we move the "windows" we need to delete the leftmost point in the lower hull, we can do it if the hull is stored in a deque. If you need more details, I can be more precise.

→ Ответить

ko_osaga

7 лет назад, # ^ |

+10

It's okay if you can explain what happens in this case :

→ Ответить

jcg

7 лет назад, # ^ |

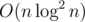Ah, I get now what yo meant before. There can be points that can be included in the convex hull when we delete the first point. If there isn't a upper bound in the length of subarray my approach should work. But we can overcome with an extra $\text{[math]}$ factor, for an $\text{[math]}$ solutions, not so nice tough. The idea is add a point to the convex hull where it can be candidate, we can do it building a segment tree where each node is an lower hull, for query a point we only have to calculate the optimums point in O(logn) hulls. Sorry, it was my mistake.