komendart's blog

Editorial Codeforces Round 445 (and Technocup 2018 — Elimination Round 3)
By komendart, history, 7 years ago, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +83
  • Vote: I do not like it

Comments Comments (56)
| Write comment?
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Editorial for Problem B Div2 is not translated into english.its showing russian version

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

This is a fast editorial, thank you!

I noticed my approach differed from the expected way in problem div2 C.

I solved it greedily: if a room that was explored at time ti exists, then do not add to the answer, but update that room so that it is explored at time i. (since you revisited) Otherwise, increment the answer by one and then create a new room visited at time i.

Here is the code: 32262674

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I also tried the greedy solution, but it seems that my implementation failed :(

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Same happened with me. :( The editorial solution is better though.

      → Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

I am not able to understand div-2 D clearly. Can anyone please explain?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    Your resultant string can not contain similar letters. For example, if you have "aba" where 'a' appears two times, it is already impossible to construct a string where "aba" will be the most frequent string. Now, using this fact, let's build a graph on letters of our strings. If we have a string "curd", that means we need to create 3 edges {'c' -> 'u', 'u' -> 'r', 'r' -> 'd'}. If such directed graph does not contain loops, just restore strings and output them in lexicographical order

    → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +11 Vote: I do not like it

After reading this three times, it still doesn't make any sense "Let us note that projection of set of points to line move center of mass of initial set to center of mass of initial set to center of mass of projections multiset" I think it should be that "Let us not that the projection of the set of points to the line moves the mass center of the initial set to the mass center of the projected points". This is in the solution of div1D

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    were you able to understand it ? if so please share

    → Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

The definition of D(N) in 886E is a bit confusing. It may be better if it is written in the following way.

Define D(n) as the number of good permutations of length n that have pn = n.

Anyway, thanks for the nice editorial. It is too bad that the contest is unrated(undated?), but I liked the problems.

→ Reply
»
7 years ago, # |
← Rev. 7   Vote: I like it +1 Vote: I do not like it

When I got my code on Problem D accepted after the contest, it was more than 100 lines. I was thinking that I finally got accepted and was satisfied. But then when I saw another one's code: http://codeforces.me/contest/890/submission/32272491 It has just 40 lines!!! I was shocked. However, reading that piece of code made me think about the logic of my code and found that there was a lot of redundancy. Then I improved my code and it became less than 60 lines. I feel really lucky about the fact that we can read others' code on Codeforces.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem D div 2, how should we print the anwser if we got the graph?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If there are cycles, answer is NO. Otherwise, restore all strings and output them in lexocgraphical order. 32280888

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you explain how to restore all string? Reading code is hard for me.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Well, your graph should be like a chain. If it is, just start to restore a string from a top of this chain one by one.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

A small addition to the 886C editorial, you also need to add 1 to the summation because the first room is NOT incorporated in the summation. This is because every term of the summation is a result of adding an "extra" room when a particular 'time' reappears in the array, ans since the first room is not added as "extra" room, it is therefore not a term in the summation. So the answer should be: ans = ans + 1

→ Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

"If there is cycle in such graph then good string doesn't exist." in Div2 Problem D.Didn't quite get it .... Can anyone explain ?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    If it were so then the occurrence of a character would be more than once.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +2 Vote: I do not like it

In Div I B, why 2nd test case can't have kekpreceqcheburek as answer. If I am not wrong this string contains kek, preceq and cheburek one time which is the most frequent count.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    According to the question , A string (not necessarily from this set) is called good if all elements of the set are the most frequent substrings of this string.

    Here "kek" , "preceq" and "cheburek" are not the most frequent substrings of "kekpreceqcheburek". The most frequent substring is "k" with frequency 3. Hence it is not good

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      OK, it means that any substring will have part in maximum frequency. I missed that part. If you have solved can you explain me your solution.

      → Reply
»
7 years ago, # |
  Vote: I like it +4 Vote: I do not like it

You have a typo in analysis for 886 E. The last factorial is right only in the second line, in the first and the third you should fix it to (h-1)!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How do you derive that equation? Can you show us?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      First addendum is the number of permutations where number n — 1 is among the first n — k — 1 numbers, all of this permutations are good. There are (n — k — 1) ways to place n — 1 and (n — 2)! ways to place every other number from 1 to n — 2.

      The second addendum is the number of permutations, where n — 1 comes at the h-th place, h >= n — k. Such permutation is good if its prefix of size h is good. So when we decide which numbers appear among the first h — 1, the number of such permutations is D(h) * (n — h — 1)!, because the n — h — 1 numbers between n — 1 and n can come in any order. There are C_n-2_h-1 ways to pick h — 1 numbers from the n — 2. So the result of multiplying is D(h) * (n — h — 1)! * (n — 2)! / (h — 1)! / (n — h — 1)! = D(h) * (n — 2)! / (h — 1)!

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +9 Vote: I do not like it

      I will also translate my another comment.

      To find the final answer let's fix where n is placed in the permutation. Let it be the i-th position in 1-indexation. Then the number of such permutation is the number of ways to pick up and place the numbers that come after the i-th position multiplied by the nomber of good permutations of size i, which is D(i). The first multiplier is C_n-1_i-1 * (n — i)! = (n — 1)! / (i — 1)! So, the answer is sum_1_n[D(i) * (n — 1)! / (i — 1)!].

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Very thorough explanation!!! I understand it now. Thank you

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +28 Vote: I do not like it

      Thanks, huesoss. I just want to put your explanation in easier to read format.

      First addendum is the number of permutations where number (n - 1) is among the first (n - k - 1) numbers, all of this permutations are good. There are (n - k - 1) ways to place (n - 1) and (n - 2)! ways to place every other number from 1 to (n - 2).

      The second addendum is the number of permutations, where (n - 1) comes at the hth place, (h ≥ n - k). Such permutation is good if its prefix of size h is good. So when we decide which numbers appear among the first (h - 1), the number of such permutations is D(h) * (n - h - 1)!, because the (n - h - 1) numbers between (n - 1) and n can come in any order. There are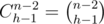 ways to pick (h - 1) numbers from the (n - 2).

      So the result of multiplying is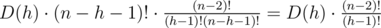

      To find the final answer let's fix where n is placed in the permutation. Let it be the ith position in 1-indexation. Then the number of such permutation is the number of ways to pick up and place the numbers that come after the ith position multiplied by the number of good permutations of size i, which is D(i). The first multiplier is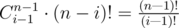 . So, the answer is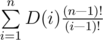

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In div 2 D, can anyone explain why we are checking that all the characters of initial strings should be presented in our answer String. I mean that if we are doing dfs for all characters, then why we need to check it separately? If we do not check it, it is giving WA on test 24.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    "A string (not necessarily from this set) is called good if ALL ELEMENTS of the set are the most frequent substrings of this string." And it looks like the path found by your dfs doesn't include ALL characters (and sequence of characters) from the set. E.g. 't' whereas the string you found is "crehpuqmbao"

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I am asking for the same reason. Why doesn't it include all characters even though we are checking for the dfs for all character.

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You start dfs only from the characters that have a zero number of incoming edges. If there is a cycle, then you won't start dfs on it.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      But for the cycle,the answer is already "NO". So,if there has been any cycle,we won't have reach at that step. I hope you are getting my point. Edit : Understood.Thanks a lot.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        If the test case is just string "aba", then you have a cycle with no entry point, so you won't start dfs and figure out it was a cycle. You check that the answer is not empty, but if the input is "aba, xyz" then you will get "xyz".

        → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

If some string is the most frequent then all its substrings are the most frequent too.

Where in the problem is this stated guys ?

For example if the n=1 and the string is aba why can't we construct the string as aba because the statement only requires the string in the set to be the most frequent substring

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    It's inferred, not stated in the problem. Try the opposite statement: 1. Assume a string "aba" in the set is the most frequent. Inside it there is a substring that appears more than once: 2 "a" => then "a" appears more times than "aba" in the result string. => "aba" is no longer the most frequent string. Hence, the most frequent string (or all strings in the set) must have no duplicated substring in itself, i.e. every substring in it appears at most once. In short, any substring in the most frequent string(s) is only allowed to be inside any one string at most once.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I'm having trouble with div2(D): the case:

2 ab ac

Should give a NO however, this graph does not contain cycles

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    There is a condition that all letters coming right after/before the same letter must coincide.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it -8 Vote: I do not like it

      Why doesn't the editorial say so then? :/

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        because then the occurrence of the substring will be 0

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It is stated in the editorial, point no.2:

        • "If string ab or similar is the most frequent then letter a is always followed by letter b and b always follow a."
        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In D, why is 2 ab ba impossible, why can't we form abba or aba?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    abba: occurence(b) = 2 > occurence(ab) = 1

    aba: occurence(a) = 2 > occurence(ab) = 1

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      So what if occurence of(b) is 2? I mean, we have 1 substring ab and 1 substring ba. Did i missunderstand?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it 0 Vote: I do not like it

        Then "a" and "b" are the most frequent substring, but we expect the "ab" and "ba" to be it.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          But a and b are not in the set

          UPD: I understand now, misunderstood problem

          → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Also, map can be replaced with binary search

Could you elaborate on that? I don't really understand what it means.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    were u able solve div1d? whats the idea behind the solution..the editorial is not even remotely helpful

    → Reply
»
7 years ago, # |
  Vote: I like it +21 Vote: I do not like it

It is high time Codeforces started caring about the variation of English used in editorials. I usually don't mind small mistakes, as long as the meaning is not completely lost somewhere inside this modified grammar/vocabulary.

→ Reply
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Were I can take the author solutions?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can somebody please explain my why solution at 886E should be correct?

for N = 5 and K = 1

we have d1 = 0, d2 = 0, d3 = 1, d4 = 5 and d5 = 23, but with the formula above you get d5 = 26... d5 = (3! * 3) + 5 * (3!/3!) + 1 * (3!/2!) = 18 + 5 + 3 = 26.... L.E. I got it wrong...

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In div 1 E solution, can anyone explain hint 1 thoroughly? I didn't understand the state (i, r, k) and the transitions. Also if possible, provide some motivations behind this approach?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can some one explain 889E solution. I figured out the O(n2) solution but i'm unable to speed it up using that suggestion in the "hint3".

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Just do the O(n^2) dp with map. It is O(n log n log C)! Since we all know that one number will be zero after log(C) times mod (one mod will make it below that half) and we also notice that if the num was smaller that the mod we now is calculating , we must keep it unmoved. (We can use a lower_bound to keep the complexity right). So what's the time to get all these numbers to 1 using mods? certainly(n log C) and each time we use log n time to discover it. We can optimize the algorithm in this way.

    → Reply