BledDest's blog

Educational Codeforces Round 32 — Editorial
By BledDest, history, 7 years ago, translation, In English
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
  • Vote: I like it
  • +74
  • Vote: I do not like it

Comments Comments (31)
| Write comment?
»
7 years ago, # |
← Rev. 2   Vote: I like it +91 Vote: I do not like it

I liked this round. Generally, the idea of educational rounds is very good. That one in particular expanded my horizons. Usually, when you learn MST, you think: "Why should I bother with Prim's or Boruvka's algo? Just learn Kruskal and forget about the rest". Task G reminds us that every algorithm is important and can have its own unique application.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +53 Vote: I do not like it

    Before this round, I didn't even know about the existence of Boruvka's algorithm.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +23 Vote: I do not like it

      Neither did I.

      Educational Rounds always teach us about some cool new algorithm or an application of an old algorithm that is not quite popular. :-)

      → Reply
    • »
      »
      »
      22 months ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Is Boruvka Algorithm same as Prim's Algorithm ?

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +29 Vote: I do not like it

    FWIW, you can solve this by starting with Kruskal's algorithm too. If you only look at the highest bit at b = 29, and split your vertex set into two halves V0 and V1 (one with all vertices where bit b is turned on, the other all the vertices where this bit is turned off). It follows that internal edges in either V0 or V1 will have bit b turned off, but edges between the two components will have this bit turned on. Thus, if you were to run Kruskal's algorithm you would first enumerate all internal edges in V0 and V1 before considering edges between the two components. It follows that Kruskal's algorithm would first connect all of V0 into a single tree (V1 respectively), and then find a single connecting edge between the two components.

    This gives you a simple recursive algorithm: Split on the highest order bit b, solve these two halves recursively (only considering bits  < b), and then find the weight of the single connecting edge, i.e. given two sequences of values, find the pair of values with minimal exclusive-or. This last problem can be solved using a very similar recursion.

    Code: 32170476

    → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Hey guys! Here are some of my thoughts on the meet-in-the-middle techniques on problem E: http://robezhang.blogspot.com/2017/11/meet-in-middle-technique-on-educational.html Feel free to ask questions and give suggestions!

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Why don't you put your implemented codes with the tutorial?I think it will be helpful for many of us :)

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem C can someone explain this part:

" Write down lengths of segments between two consecutive occurrences of this character, from the first occurrence to the start of the string and from the last to the end of the string."

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +12 Vote: I do not like it

    Let k be the maximal length such that there exists segment of length k that doesn't include character c. You can take all the occurrences of character c and check where this segment can fit. Thus maximal distance between those occurrences and ends of the string will get you maximal k.

    → Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Look at my codes for the problem F. I wrote a solution using an algorithm Boruvki but unfortunately it got TLE. Even though my realization is not good as author might have expected to see, I think 2 seconds for the problem which has complexity of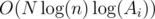 is (very) tight

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Try first sorting numbers. I have no idea why it works, but I also had time limit with same solution and sorting the numbers mad code at least 2x faster.

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Doesn't the Boruvka's algorithm work for graphs with distinct edge weights only? In the case of problem G, how is that guaranteed?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +12 Vote: I do not like it

    It is not guaranteed, hence the warning.

    but we should be careful to avoid adding edges that form cycles in MST

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you please elaborate how is the repetition avoided ??

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +5 Vote: I do not like it

        The problem is with duplicates. Instead of dealing with just weights of edges, consider the pair (w, i) for each edge, where w is its weight and i is the edge index. Now no two pairs are same as each edge has a different index and you can run Boruvka's algorithm as usual.

        Code

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

If I understand correctly, the editorial claims that the answer for B is always n — dx — dy. Can someone prove it mathematically? How about an intuitive proof?

Was just trying to figure out how I can come up with such ideas myself in the future. This sounds like a genius idea to me but I am not sure why it works.

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Problem G can be simply solved by trie with 2 keys 0 or 1.

Complexity = O(n * (30 or max(log ai))

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why is the time limit so strict for G? I'm almost using same solution as Editorial, and it takes ~2300MS to pass all test cases, but time limit on CF is 2000MS.

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why A problem have a tag 1600? There is very simple.

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone explain 2-D dp solution for problem D. Almost Identity Permutations ?

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I love G so so much. I have the same thought of the solution in mind but I didn't think it could run in time. But when I saw the editorial I was very exciting. It actually made me love the CP again even this problem is pretty old. Thank you, the author and Codeforces.

→ Reply
»
3 years ago, # |
  Vote: I like it 0 Vote: I do not like it

why problem D has dp as one of its tag , it has nothing to do with the dp i guess just simple permutation n combination !!

→ Reply
»
2 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem G (Xor-MST), you don't really need to know Boruvka's algorithm. In fact, I don't really understand what the editorial is saying, but that's okay :D.

Just make a binary trie and all in all of the $$$a_i$$$. Then, for each subtree in our trie, we need to know the minimum cost to to conjoin everything in the subtree. For each node, we store this minimal cost. If we have some node and it has only one child, then the cost for that node is the cost of the child. If a node is a leaf, then it's obviously cost 0 too. If the node has two children, then the cost is sum of costs of children plus cost to join children. To find cost to join children, iterate over stuff in the left subtree and find best corresponding child in right subtree (idk if this makes sense).

→ Reply