-synx-'s blog

Splay Tree Problem — Can it be solved using Order Statistic Tree?
By -synx-, history, 7 years ago, In English

http://www.spoj.com/problems/ADALIST/
The problem asks to efficiently perform insert/erase/index at kth position!
I know it can be solved using Splay Tree easily in O(nlg(n)).
My question however is can we use Order Statistic Tree (PBDS) to solve it too? (inserting might cause issues, I think)

  • Vote: I like it
  • +10
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

I think it is not possible, because the elements in pbds::tree must be sorted.

But I get accepted by using ext/rope. https://www.sgi.com/tech/stl/Rope.html

(it is really slow.)

I did not find any way to use pbds' internal functions.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

ask for index = build splay tree on values

ask for kth = build splay tree on positions

therefore it's not possible to do it in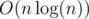

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +2 Vote: I do not like it

    No, this is a well-known problem that can be done with splay/rbtree/avl in O(n log n).

    (Friend, have you heard of sized balanced tree? This is famous in Chinese OI community. http://wcipeg.com/wiki/Size_Balanced_Tree)

    You need a balanced binary search tree, and maintain the size of subtree rooted at each node. Then you can binary search the k-th element of the whole tree.

    node *find_kth_node(node *n, int k) {
     int lsize = n->left ? n->left->size : 0;
     if (k < lsize) return find_kth_node(n->left, k);
     else if (k == lsize) return n;
     else return find_kth_node(n->right, k - 1 - lsize);
}

    (maintain the size is a very tedious work, because of the insertion, deletion, rotation, etc)

    Fortunately, ext/pb_ds have sized splay/rbtree implementation. But it does not have an interface to insert a node at a specified position (insert(position, value) or insert_before(iterator, value)).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      it's finding the kth node right?

      i am not quite understand that, i mean, how could u find the kth node's(according to the value) index and insert some node in the kth position(according to the original order) in ?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You misunderstood the problem.

        Search and insertion are both according to the index / position, not value.

        Position of k-th smallest value is not well-defined anyway, because there can be repeated values, right?

        → Reply
»
5 years ago, # |
← Rev. 2   Vote: I like it -13 Vote: I do not like it

Can I solve it through STL Vector? I didn't know the Splay tree or what you guys are telling... Can you guys suggest me some good blog upon this topic? I am stuck at this problem getting 17 TLE using vector.

→ Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If you want I can publish a blog on 32nd March on how to solve it using vectors.

    → Reply
    • »
      »
      »
      5 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      I hope You can do so. But I am extremely sure that I can be as equal as you in next 29th February**** and See you then guy.

      → Reply