Codeforces Round 440 will start on October 15 (Sunday), 08:05 (UTC). It will be based on Technocup 2018 Elimination Round 2. So, if you are a Russian-speaking high-school student, please take part in the Technocup 2018.
Codeforces Round 440 is open and rated for everyone.
Wish you good luck and bugless code.
Editorial is posted.
Congratulations to winners!
Technocup official round:
Div. 1:
Div. 2:















Mandatory comment- "Hope the problem statements are as short as this blog".
Clash with OpenCup. ;(
Is it me or is the contest title is longer than the announcement :3
I guess it's the first time that we don't see any "thanks" or even any username in an announcement :D
well it would be mike thanking himself :)
This is like the shortest announcement ever of all time.
A good time for Chinese students!
for Asian students!
And Australian!
I have an onsite contest after 15mins for 5 hours, and then I can take part in this cf round. A good time for me.
I have doubt.
When I opened 'contests' page, it showed me two separate contests(div1 and div2), but in the announcement it is given (Div1 + Div2). Which one it is going to be ? MikeMirzayanov
UPD : when I posted this comment, there were only 2 contests. (contests 440Div1 , 440Div2).
That's why I got confused. Right now contests page is fully updated. NH_Apu
dont't be stupid
I Wish everyone positive rating!
You have to be really bad to have a negative rating (like worse), so the wish is likely to come true.
And yet he's managed to disprove this
why do timing varies a lot recently ??
I hope I won't get a WA on problem A, the way it happened in the previous contest :(
In previous contest U got TLE.
It will be at 3 AM here in Colombia. Guess is a good way to start a Sunday ¯_(ツ)_/¯ .
2 PM in Bangladesh..Surely the best time except for missing lunch
The Terms of agreement when registering is in Russian "Вы подтверждаете, что будете работать самостоятельно во всех этапах Технокубка и не будете нарушать какие-либо другие правила." So I'm wondering whether an English version of problem statements will be given during the real contest. Can anyone explain about this a little bit? Thanks a lot.
There will be english statements
gl hf
number of problems and the difficulty is about the 1st round ? because that round was easier than ususal
What's the "Practice Round 2"?
EDIT: never mind, seems to be for Technocup official participants only
Hope there will be no geometry problems
why don't you like geometry problems?
geometry is good, it makes people cry T_T
May be it's a silly question.
but what does "00:04" like things below every submission means??
is it time of submission or what
You mean the time that is shown below the submission during the contest.
Its the time when you've submitted the solution after the start of the contest. '00:04' Would mean that you've submitted the solution after 4 minutes
How long will the contest last?
2 hrs
have no time to receive it :D
Why can I register for both Codeforces Round 440 (Div 1) and Technocup 2018 round 2?
How many problems?
YouHaveShort Blog.
Registration button didn't work for me...
Still can't register in div.2 ((
Russian-speaking high-school students have to register in this contest.[contest:http://codeforces.me/contest/870]
Mandatory comment- "Thankyou for the short problem statements".
Disclaimer: My argument may be wrong, and if it is, I don't mean to offend anyone, so apologies in advance.
The contestant who is currently second (at the time of commenting) in the leaderboard looks mighty suspicious. He has solves solves for 3 different problems in the space of 6 minutes, including solving D in 2 minutes. Check out his submissions.
How is it possible to do D problem in 2 minutes :O.Is it a joke? :|
Same case in hackerrank. People have multiple accounts, view problems from one account and once they got the solutions, they submit all at once.
That doesn't work here.
Looks like someone else submitted his C first and later he resubmitted. Look at the programs. There is no template in the first submission of C.
I think destinydrifter can explain better
It's extremely sad, given nothing has been done about this. The contestant was not kicked out of the contest, and even received a significantly large rating increase (+281). Please look into this MikeMirzayanov, KAN.
In Div-1 B, just ask n queries of the form (i, 0) and n queries of the form (0, i).
Now, if you know p[i], you can get p[j] using p[i] ^ query(i, 0) ^ query(j, 0).
And if you know b[i], you can get b[j] using b[i] ^ query(0, i) ^ query(0, j).
Now, one by one, fix the the value of p[0] from 0 to n-1. Then you can recover the whole permutation p[].
You know that b[p[0]] = 0, so you can recover the whole inverse permutation b[] as well.
Check if both are valid. All elements of p[] are distinct and 0 <= p[i] < n && b[p[i]] = i.
It this is true, this is a valid answer. Simply count the total and print any one of these.
I only stuck for checking is it valid permutation. Simply I do not see why it means that all n2 pairs will produce correct answer as valid permutation.
If you do these 2n queries all other queries are redundant.
Q(i, j) = Q(i, 0) ^ Q(0, 0) ^ Q(0, j)
Yeah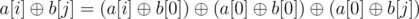 so querying these is enough.
so querying these is enough.
I did not check that p[] are distinct, but I don't think that there could be 2 the same elements.
All elements of p are always distinct in all potential permutations.
Say pi = pj. But then xor(pi, pj) = 0. Hence pi = pj in all potential permutations and there is no answer.
Besides, you need to apply this procedure only for even n. For odd n, p0 is uniquely determined, hence only one possible permutation.
My solution:
I first find the value of a[0]^b[i] for all 0<=i<n (by query(0,i)) let v[i]=a[0]^b[i] for all 0<=i<n Next, I fix the value a[0]=j, 0<=j<n Now, its not hard to produce b and the corresponding a array using the above definitions. Then, just check the validity of this solution.(All this is being done for a fixed value of j) What's wrong with this approach? I am getting WA at test 7
Since you haven't done queries of the form query(i, 0), the information you have is not equivalent to all the information you would have if you made all n2 queries.
Got it. Thanks :)
Ok, so what are the hacks on B? Thanks for short statements, by the way.
3 2 1 8 1
Depends on the solution. I used the following hack a lot for the ones who used sorting:
3 2
1 2 1
literally 1 sec from submitting D and the contest ends :/ .
How to solve Div-1 C?
Let's say that two points are connected if they lie on the same horizontal or vertical line. Find connected components. For each of them, let L denote the number of possible different lines you can draw, and let P denote the number of points.
For example, for a single point L = 2 and P = 1. For two points with the same y-coordinate it would be L = 3 and P = 2. For the sample test with four points it would be L = 4 and P = 4.
It turns out that you can draw a subset of L possible lines if and only if its size doesn't exceed P. So the answer for this connected component is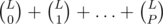 .
.
What is X?
sry, it was supposed to be P. corrected now.
Thanks! Great solution really. I was taking quite a complicated route only to arrive at the wrong formula.
I think he meant P.
You can also note that P ≥ L - 1, so the answer is either 2L or 2L - 1.
nice, missed that
But for second example, output is 9, which is neither in 2^L nor 2^(L-1) format
for each component he means that example has 2
Make a bipartite graph like this :
In one of the parts put a node for every x. And in the other part put a node for every y. Now a point in the problem at coordinate (xi, yi) is an edge in the graph that is between node xi in th first part and the node yi in the other part .
Now consider a connected component , consider that it has k nodes.
If this component has a cycle , then you can make all 2k states for horizontal or vertical lines in this component .
Otherwise when the component is a tree you can make all of the states minus the state that all the nodes (vertical and horizontal lines) appeared , so it has 2k - 1 states!
I see Div1 C smth likes ARC83 F: https://atcoder.jp/img/arc083/editorial.pdf.
Hints for Div2 E?
how to do C?? i submitted in last 3 min..
if(x&1 || x<4) ans=-1;
if(x%4) ans=x/4
else ans=[(x-6)/4]+1
for (n%4==3) (n-15)/4+1 or (n-15)/4+2??
(n-15)/4+2
why?? for 27=4+4+4+15 it's 4 not 5!!
15 is 6 + 9 :)
if (n < 4 || n == 5 || n == 7 || n == 11) cout << -1 << \n; else cout << n / 4 — n % 2;
fail for 9
there should be a "-" instead of "+"
n/4 — n % 2 is correct for all n>=12 for 1,2,3,5,7,11 ans = -1 For 4, 6, 9 ans = 1 For 8, 10 ans = 2
i misspelled it, it's a "-" there for all of the numbers, instead those cases that I wrote
"if(x&1 || x<4) ans=-1;"
This is wrong. What if x = 9?
My logic was:
if N is Even:
If N < 4: -1;
Else If N >= 4: N / 4;
else N is Odd:
If N >= 9 and N != 11: 1 + (N — 9) / 4;
Else : -1;
You logic prints out 2 if N = 11. This is wrong.
I mixed up the even and odd case. It is correct now.
every number 11 > can be expressed as sum of composite numbers
so if n<=11: you can precalculate that that
else if (n & 1) n-9,ans++
ans += n/4
31347433
wait whoops i forgot to flush output for final answer for B and i still passed pretests even though the problem warns against this, i hope i pass systest...
EDIT @below: Nope, I used '\n' to end my line, I really hope I'm okay...
maybe you used endl , it calls os.flush()
Hacks for C?
I don't know which ones where in pretests, so I'll write some special cases:
5
5
9
11
13
15
Fun solution for Div.1 D:
The main observation is that the distance for every pair is either 0, 1, 2 or 3.
You can easily find the number of pairs with distance 1 (they have gcd ≠ 1 and this is a well known problem).
For the number of pairs with distance 2 the following condition should be true:
lp(X) * lp(Y) < = n, where {X, Y} is the pair (lp(x) here is the least prime divisor of x).
That's true, because we can have a path like X -> (lp[x] * lp(y)) -> Y.
And now we are left with pairs with length 3. The following conditions should be true:
lp(X) * lp(Y) > n and max(lp(X), lp(Y)) * 2 < = n, where {X, Y} is the pair.
That's true, because we can have a path like X -> (2 * lp[x]) -> (2 * lp(y)) -> Y.
Well if we have found the number of pairs of distance 2 and we count the number of pairs for which max(lp(X), lp(Y)) * 2 < = n is true and then remove the number of pairs with distance 2 we will get the number of pairs with distance 3.
Well now the only part is how to count the number of pairs with the given two conditions. We can do a fenwick tree on the values. Here is the code.
Why is distance being further than 3 impossible?
Because for every pair {X, Y} if there is a path, then we can go like X -> (2 * lp[x]) -> (2 * lp(y)) -> Y.
Could you explain how you count these pairs with a fenwick tree a little more? Maybe it's less complex than I'm making it out to be, but I got the conditions in-contest but couldn't figure out how to count them easily.
First we do n - 1 point updates of form add 1 to lp(i).
Now we start iterating all numbers from 2 to n. Let our current position/number be i.
We remove 1 from the fenwick tree at position lp(i). Now the number of pairs with lp equal to X is the value at position X in the fenwick tree.
To count the number of positions lp(X) * lp(Y) < = n we can simply query the range [2;n / lp(i)].
For the second condition (lp(X) * lp(Y) > n and max(lp(X), lp(Y)) * 2 < = n) we will have query in range [2;n / 2] — query in range [2;n / lp(i)].
And we only add the second part to the answer (the pairs with distance 3) if 2 * lp(i) < = n.
What does cnt[i] calculate in your code?
Initially the number of numbers divisible by i. Then the number of pairs of numbers with gcd equal to i.
Ok I finally got the key part I've been missing , namely the fact that if x and y are distinct, not coprime and at most n then the product of the smallest prime factor of both numbers must be at most n.
Proof : Let g be the gcd, then if g does not exceed sqrt(n) we're done. Otherwise, let x = ga, y = gb, and wlog b > 1. Then, the product of smallest prime divisors is at most gb which is at most n.
I don't think we need BIT here.
To find the number of pairs for which lp(i) * lp(j) <= n, just store the prefix frequencies of the lp array. Then for every i, add pref[n / lp[i]]. Remove the number of i, such that lp(i) * lp(i) <= n, and divide by 2.
Link
You're right. Idk why I didn't see that.
Thank you for this solution. I would like to add that it can be adapted to O(n) by using two pointers instead of Fenwick trees. Code : 31374591
Does any one solved problem div2 C using DFS / BFS or Recursion or dp ?
I used greedy: keep subtracting 4 from the number.
If n % 4 == 1: Use 9 as your composite number.
If n % 4 == 2: Use 6 as your composite number.
If n % 4 == 3: Use 15 as your composite number.
This is the rough idea behind the problem.
you mean use 6 and 9 as composite numbers if n%4==3
Yes, my bad. :P
I did assign a count of 2 to 15, so my final answer is fine.
I tried solving it using recursion , got TLE @test case 7
The number can be up to 10^9. What did your recursion do, exactly?
i solved using dp. Greedy till certain point ( ~5000), dp in the end.
May be rename to Mathforces?
For some reason, for Div 2 C I thought that the queries themselves had to be prime to be valid, and I would need to print out -1 if the queried number wasn't prime.
I wrote up the entire code of getting all the primes less than sqrt(1 billion) by checking for primality with a sieve. Then I checked for each query number if it was not prime by seeing if it could be divided by any of these prime numbers < sqrt(1 billion) I found through the seive, and then I realized I had interpreted the problem wrong and had added more requirements than necessary!
Anyway, how did you check primality of numbers up to 1e9 using sieve, not miller-rabin?
I found all the prime numbers less than sqrt(1e9) using a sieve. There were about 5,000 or so I think.
I stored all these primes in a vector.
And to check whether each queried number N was prime, I just iterated through the primes and checked if any of them could divide N.
This would come out to about 5 * 1e8 time.
Thanks. An offline method, interesting :)
waiting for system test.
When will the system test start?
Come on, khadaev. We agreed to submit on 1:30 -_-
cheaters xD
How to solve div.2 D? It's it about circles of permutation?
It's about n^2 brute-force. You can query (0..n-1, 0) and (0,0..n-1) and try every position of b0, say fix b0=i.Then reconstruct p from pi=b0^(saved query(i, 0) value). Finally, check whether it is a valid permutation and consistent with the queries.
Er...set b0 to i?Are you mean that assume b0 is i,then Query(0,0-n-1) and Query(0-n-1,0)...?
It seems good...But how to construct all the p values or determine the value of the true b0...?
Sorry for my late reply and my low intelligence...
Let Q0, Q1 be arrays of length N and Query(X, Y) be query value — i.e. P[X] xor B[Y].
We can save Q0[i] = Query(i, 0) and Q1[i] = Query(0, i) for all 0<=i<N.
Then the brute force begins.
We fix b[0] = k
We can reconstruct P by setting P[i] = Q0[i] xor k.
Now we check whether P is a valid permutation.
If it is valid, then we check P against our saved queries, namely Q1.
5 Repeat from 1 to 4 for all 0<=k<N.
I think div.2E is a problem of combination number,but I can't get the solution.
Div.2D: I wrote all my queries to stdout and flushed, then read the all of the answers one by one, and my submission got an ILE? Somebody wrote one query to stdout and then read the answer at once, then he passed the pretest? Is it my fault? My Submissions:
cstdio version
iostream version
Practice submission(query and then read at once):
Practice version
del
На прошлом раунде взяли 100 человек, так что еще неизвестно )
I submitted solution to B after hack to my solution which got accepted. To recheck it i submitted my previous solution again and it showed the wrong answer. Now my solution (correct one) is not getting evaluated. Will they not consider my correct solution. :( EDIT : They evaluated it :)
NOOOOOOOOO!!!!!!!In Div2 D During the contest I read the answer of 2*n times together and I got an ILE…… After contest I tried read every answer after questioning I got AC …… Oh my goodness……
Same thing happened to me, which wasted me 30 minutes and 7 incorrect submissions = almost 500 points.
How to solve Div.1 E?
I think the main problem is constructing compressed tree for that k vertices. I remember it is to solve this: https://open.kattis.com/problems/optimistan.
Pick a pair of special vertexes U,V that are as far from each other as possible. Construct a chain that connects them (these are the points with d(U,W)+d(W,V)=d(U,V) ordered by distance from U). Consider subtrees rooted at each vertex from this chain. We can easily split all vertexes into these subtrees. The distances to each vertex X from X's root Y equals to d(U,X)-d(U,Y). So we may treat roots as special vertexes. Most of subtrees will have only one special vertex — the root. They may be processed in O(N) in total. For the other subtrees we recursively call the same procedure.
This process seems to terminate quickly. On every step each subtree will lose 2 special vertex, but it may possibly generate some new. The more subtrees there are, the faster the special vertexes are lost. It seems all vertexes will be processed in O(K) iterations and problem is solved in O(KN).
Good, lucky problems, good contest as well as author!
My screencast
Hope you find it interesting!
For problem B
for k==2 how is it max(a[0],a[n-1])
Seeing, that you can achieve it, is pretty easy. You can take that one element as one segment, and the rest as the other.
Let's assume we achieve an answer x such that x > max(a0, an - 1). If this element is in the first segment, then the first segment's value should be x, but since x > a0 the score will be at most a0. Same goes for the second segment, so x can be in neither segment, which is contradiction.
Splitting of array a of n elements into 2 subarray,it must be a prefix and a suffix. for the minimum to be larger, we make the 2 subsegments [0,n-2] and [n-1, n-1] or [0, 0] and [1,n-1]
subsegment can be:
[0,n-3][n-2,n-1] like that...
why these two??
2 subsegment : [0, x], [x+1, n-1] (0 <= x < n-1)
the answer is max(mininum in [0, x], mininum in [x+1, n-1])
so :
mininum in [0, 0](it is a[0]) is larger than mininum in [0, x]
mininum in [n-1, n-1](it is a[n-1]) is larger than mininum in [x+1, n-1]
when a[0]>a[n-1] a[0] is larger than mininum in [0, x] and mininum in [x+1, n-1](for each x : 0 <= x < n-1)
when a[0]<a[n-1] a[n-1] is larger than mininum in [0, x] and mininum in [x+1, n-1](for each x : 0 <= x < n-1)
so for the minimum to be larger, we make the 2 subsegments [0,n-2] and [n-1, n-1] or [0, 0] and [1,n-1]
sorry, my English is not very good, but you can try to understand it. :)
Oh..There are so many hacks today! You see There are about one thousand and seven hundred people solved ABC during the contest. So do I. But my solution for B got a FST... Because I defined the mininum by -1e9+7 instead of -(1e9+7).. But I still got rank 180..Because I hacked eleven people :P
Will there be an editorial?
http://codeforces.me/contest/872/submission/31353320
check this solution for Div2D.
When something likes "5000 xor 4191" happens, will it get Runtime Error ? I think it will
but why it didn't happen ?
I think you don't need to do this. I'm just lucky. :)
Is the editorial published ?
How you guys came up with Div2-C . I mean is it writing bruteforce than generalizing it Or there is some other way to approach for solution?
I will try to explain a possible approach.
First, if you want to represent n as a sum with lots of summands, those summands have to be small. Therefore you should ask yourself, what is the smallest suitable summand? It is 4. Can you use only 4? Only if n % 4 == 0. What about the other remainders modulo 4? You are obliged to use something else apart from 4.
The next composite number is 6. You can see that if n % 4 == 2, using one 6 and all 4 is optimal. But you cannot obtain any odd n using only 4 and 6.
Hence you need to use one more number. Maybe 8? No 8 is not useful as 4+4=8. Maybe 9? Yes! Using one 9 and all 4 you can obtain all n % 4 == 1.
The only remaining case is n % 4 == 3. Can you get it using only 4, 6, 9? The answer is yes as 6 + 9 % 4 == 3. The issue is that this is no more trivially optimal and you have to check the optimality. However, checking it is super-easy, as the smallest useful number (i.e. it is composite and it cannot be generated as a sum of 4, 6, 9) is bigger than 6+9 = 15 and therefore using 6+9 is optimal if n % 4 == 3.
p.s. I have ignored all small cases. As a byproduct of the explanations I have given ,those are all impossible (1, 2, 3, 5, 7, 11).
And how many participants went to the final?
Does anybody know why I receive "Denial of judgement" for sources 31428657 and 31428722 ? The error on test 88 is : Can't compile file: Compilation process returned error: execution failed because of unknown invocation error