Number of distinct integers in two subarray

7 years ago, # |

← Rev. 2 →

+12

The query can be transoformed into (number of distinct elements in [L₁;R₂]) — (number of distinct elements in [R₁ + 1;L₂ - 1] which don't occure in [L₁;R₁] and [L₂;R₂]).

The first part is the well known SPOJ D-query and the second one can be solved by dividing the elements in heavy and light by the number of their occurrences (lets consider numbers heavy if their occurrences in the whole array are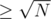 $\text{[math]}$ and light overwise).

The number of heavy groups is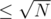 $\text{[math]}$ so for every query we can check if every heavy number satisfies the second part of the inital query (in O(1) or $\text{[math]}$ ).

Now for the light numbers it will be a bit trickier. For each light group we can itterate over all pairs of numbers (because the group size is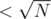 $\text{[math]}$ ). To solve the light group part we will consider every pair of positions and add a tuple (i, j, lsame_i, rsame_j), where i is the left position of the pair, j is the right one, lsame_i is the closest position to the left with same number and rsame_i. Now to answer the query we need the number of tupples with 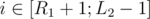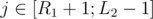$\text{[math]}$ , $\text{[math]}$ , lsame_i < L₁ and rsame_i > R₂. And so the building of the structure will be 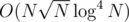$\text{[math]}$ and the query will be in 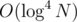$\text{[math]}$ if we do a 4d Fenwick. If we change the size of the consideraton of the groups (currently 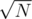$\text{[math]}$ ) we can achieve 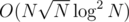$\text{[math]}$ for building and 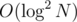$\text{[math]}$ for query for the light.

And so here is a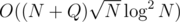 $\text{[math]}$ solution.

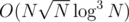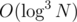PS: We actually can use another structure for the light queries which looks like a 2d Fenwick with a persistent segment tree in it. This way the building and query will be $\text{[math]}$ and $\text{[math]}$ . With careful choosing of the size of consideraton of the groups we can achieve a 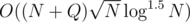$\text{[math]}$ solution.

PS2: The chance of this solution being a complete overkill isn't small.

→ Reply

7 years ago, # ^ |

+15

wow ! the solution confused me a lot :)

maybe I have to read it many times and maybe a code can help me in understanding :)

can you ( or anybody else ) share its code please ?

→ Reply

Kerim.K

7 years ago, # ^ |

But the time complexity near to N * Q.

→ Reply

7 years ago, # ^ |

yes ! For N = 10 ^ 5 and Q = 10 ^ 5 time is 182 seconds :|

→ Reply

7 years ago, # ^ |

Actually the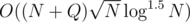 $\text{[math]}$ solution will do about 2 billion operations and should be able to run in about 5-10 seconds if implemented well, while the O(NQ) will do about 20 billion operations (which are simple though). I'm not sure if you are able to pass below a minute with the O(NQ) solution.

→ Reply

7 years ago, # ^ |

← Rev. 3 →

Naive O(NQ) runs 12.5 seconds on CF servers, and I think I can make it work less ~~than 5~~ than 10 seconds. But I'm really not sure that you can implement your solution so that it will run for less than 10 seconds =)

→ Reply

geniucos

7 years ago, # ^ |

How do you know? Is this problem anywhere on CF? No link is provided in the blog

→ Reply

7 years ago, # ^ |

Custom Invocation. My code: https://pastebin.com/6w5EgaTj

→ Reply

7 years ago, # ^ |

Doesn't codeforces custom invocation kill solutions after they have ran over 10 seconds?

→ Reply

7 years ago, # ^ |

← Rev. 3 →

+16

It does. But I run for Q = 10k, 50k, 70k, etc, As my code runs O(N) per query you can easy calculate the time for 100k =)

~~btw, I think I have easy O(NlogN). Will describe in 1-2 hour, when come home~~ I was wrong. Sorry.

→ Reply

7 years ago, # ^ |

No the problem formed in my mind :)))

→ Reply

https://pastebin.com/KBKQrDMw

7 years ago, # ^ |

~5 seconds with O(NQ)

→ Reply

RockyB

7 years ago, # |

← Rev. 2 →

I know O((N + Q) * log2(N) ^ 3) solution :)

UPD1: Building O(N * log2(N) ^ 3), Query O(log2(N) ^ 3)

→ Reply

7 years ago, # ^ |

Can you share it?

→ Reply

7 years ago, # |

Auto comment: topic has been updated by nima10khodaveisi (previous revision, new revision, compare).

→ Reply

dacin21

7 years ago, # |

← Rev. 3 →

+37

A solution in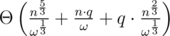 $\text{[math]}$ with bitset should be squeezable, assuming the memory limit is large enough. (ω, the word size, is usually 32 or 64).

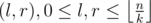Compress the a_i to be in [0, n - 1]. Let $\text{[math]}$ be the block size. For every pair $\text{[math]}$ precompute a bitset storing 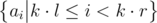$\text{[math]}$ . T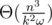his takes $\text{[math]}$ time and memory.

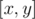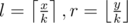To get the bitset of any range $\text{[math]}$ , let $\text{[math]}$ . Get the precomputed bitset for (l, r), then add the values in a[] from x to min(y, k·l) and from max(x, k·r) to y into the bitset. This takes Θ(k) time per query.

The answer to any query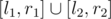 $\text{[math]}$ is (get_bitset(l₁, r₁) | get_bitset(l₂, r₂)).count(). This takes 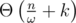$\text{[math]}$ time per query.

A factor 2 could be optimized by considering numbers that appear only once in a separately, which cuts the size of the bitset in half.

Edit: fixed formula for k.

→ Reply

7 years ago, # ^ |

← Rev. 2 →

oh okay :) interesting solution :))))

But I think time is not ok :)

→ Reply

Kerim.K

7 years ago, # ^ |

But I think memory is not ok :)

→ Reply

7 years ago, # ^ |

maybe problem hasn't better solution :)

→ Reply

7 years ago, # ^ |

← Rev. 2 →

It is ok actually. The memory will be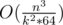 $\text{[math]}$ where k is the block size. This way we can set k to 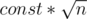$\text{[math]}$ to fit the memory limit. This way our time complexity will increase by a constant factor but it won't be a big constant (about 2 or 3).

→ Reply

dacin21

7 years ago, # ^ |

+15

Thanks for commenting with the proper memory consumption (should be fixed now).

Custom test runs in 1715 ms, using 125'192 KB (without the optimisation)

Code

#include <bits/stdc++.h>
using namespace std;
constexpr int maxn = 100000;
constexpr int block = 1000;
bitset<maxn> pre[maxn/block+1][maxn/block+1];
signed main(){
    int n, q;
    cin >> n >> q;
    mt19937 rng(643);
    auto get_rand = [&](int l, int r) {
        return uniform_int_distribution<int>(l, r)(rng);
    };
    vector<int> v(n), s;
    for(auto &e:v) e = get_rand(0, n-1);
    for(int i=0;i<n/block;++i){
        for(int j=i+1;j<=n/block;++j){
            pre[i][j] = pre[i][j-1];
            for(int k=block*(j-1);k<block*j;++k){
                pre[i][j][v[k]] = 1;
            }
        }
    }
    
    auto get_bitset = [&](int const&l, int const&r){
        if((l+block-1)/block >=r/block){
            bitset<maxn> ret;
            for(int i=l;i<=r;++i) ret[v[i]]=1;
            return ret;
        } else {
            bitset<maxn> ret = pre[(l+block-1)/block][r/block];
            for(int i=l, lmax = (l+block-1)/block*block;i<lmax;++i) ret[v[i]]=1;
            for(int i=r/block*block;i<=r;++i) ret[v[i]]=1;
            return ret;
        }
    };
    
    const int K = 40;
    long long ans = 0;
    while(q--){
        int a, b, c, d;
        a = get_rand(0, n / K); b = n / 2 - get_rand(0, n / K);
        c = n / 2 + get_rand(1, n / K); d = n - get_rand(1, n / K);
        ans+=(get_bitset(a, b)|get_bitset(c, d)).count();;
    }
    cout << ans << endl;
}

→ Reply

7 years ago, # ^ |

Actually the number of operations for given constraints is about 300 million simple operations which should run in less than 3 seconds (it can be even faster).

→ Reply