wish_me's blog

Recursion Problem.....:)

By wish_me, history, 7 years ago, In English

Given 3 characters a, b, c, find the number of strings of length n that can be formed from these 3 characters given that; we can use ‘a’ as many times as we want, ‘b’ maximum once, and ‘c’ maximum twice

  • Vote: I like it
  • -10
  • Vote: I do not like it

Comments Comments (10)
| Write comment?
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can you describe what is your approach to solve this problem?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I tried to solve it recursivly by generating all possible strings and then discarding those strings which doesn't follow above rule?

    Can you tell me more efficient approach?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      How about using permutaions?

      1. Number of strings containing only a's.

      2. Number of strings containing 1 b and rest a's.

      3. Number of strings containing 1c and rest a's.

      . . .

      and add the sum of all the above points to get the final answer.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        then how to print them in minimum complexity?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          The best you can do is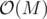 where M is the number of possibilities. To do it efficiently, make some string of length n, and recursively fix the character. You'd do this from left to right, and your recursive function should pass down information on whether or not you've fixed the letter b, and how many c's you've fixed so far.

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            thanks a lot sir.Can you write pseudo code?

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
              ← Rev. 2   Vote: I like it 0 Vote: I do not like it

              Not too hard:

              s = std::string(n, ' ');

def rec(i, bs, cs):
    if i == n:
        print s
    else:
        s[i] = a
        rec(i+1, bs, cs)
        if bs < 1:
            s[i] = b
            rec(i+1, bs+1, cs)
        if cs < 2:
            s[i] = c
            rec(i+1, bs, cs+1)

rec(0, 0, 0)
              → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I assume you're solving this, since N<=20 you can use:

Spoiler
→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

There aren't many possible cases if we care only about 'b' and 'c'. Let's focus only on placing 'b' and 'c', the remaining will be 'a':

1) no 'b' and 'c': 1 option.

2) only 1 'b': n options.

3) only 1 'c': n options.

4) 2 'c': n(n — 1) / 2 options.

5) 1 'b' and 1 'c': n(n — 1) options.

6) 1 'b' and 2 'c': n(n — 1)(n — 2) / 6 * 3 = n(n — 1)(n — 2) / 2 options.

so to sum it up, given n you need to output: 1 + 2n + 3n(n — 1) / 2 + n(n — 1)(n — 2) / 2.

this is O(1) which means it's slightly faster than an exponential complexity by using recursion.

→ Reply