szawinis's blog

Help with problem
By szawinis, history, 7 years ago, In English

You are given two arrays of integers a, b both with length n <= 10^5. For each 0 <= x <= n print the sum of a[i]*b[x-i] for all 0 <= i <= x.

It's obvious this can be done in quadratic time, but can we do any better?

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it +6 Vote: I do not like it
Hint: two questions
Answer to first question
Answer to second question
→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Thanks for the reply. Your strategy is quite interesting, however that only solves the problem if we want the sum over a[i]*b[x-i] for all x and for all i. The problem was to isolate each x and calculate the sum over a[i]*b[x-i] for all i for this value of x only, then move on to the next value of x. I'm very sorry if this wasn't clear.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Oh, I didn't get that. I think that the same strategy works in this case though.

      → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

It seems that the answer will always be equal to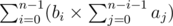 . (can't prove it, sorry)
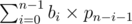Let p be the partial sum array of a. Then the answer is simply .

→ Reply