I was trying to solve this problem which recently appeared in a hackerrank contest. The editorial mentions a solution based on geometric interpretation of the question.But since a lot of tree path questions can be done using centroid decomposition,does anyone know how to solve it using centroid decomposition?
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 154 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2025 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Feb/22/2025 11:01:43 (i2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










You can use centroid decomposition and persistent segtree, although I definitely do not recommend it.
Code
Can you explain your solution briefly?
Given a tree, you want to compute the number of paths through its root r which are not special. First enumerate the nodes of the tree in order of depth first search.
We can use a persistent segment S tree for each node a, where S[b] = 1 if the path a - b is not special and S[b] = 0 otherwise. With this segment tree, we can
Note that the sum of all elements in the segment tree will be equal to the number of non-special paths passing through r with the first endpoint at a.
Suppose that the path a - b passes through r and is not special. Then obviously if c is a child of a, then the path c - b is also not special. So the segment tree for c will be the same as that for a, except a possible range modification.
This is a really interesting solution. Thanks for the explanation!
On an related note, what is the rationale of adding hackerrank contest to codeforces calendar. The '101 Hack' is added to the calendar. However the OpenBracket and GoldmanSachs codesprints are not added.
I feel the calendar consists only short contests may be . And that is good because if we want all contests we can refer clist.by
I don't know about OpenBracket ... but Goldman Sachs is an unrated contest ... Maybe only contests which are held by HackerRank for rating points in their website (and not hiring challenges) are added.
I have a solution without centroid decomposition, but it seems that it might be possible to adapt that solution for CD :P.
Suppose we want to know the number of special paths starting from some vertex v. For all vertices w, let's colour w black if and only if on the path from v to w there is another vertex with the same label as w. It is obvious that then, the answer is the size of the maximal connected subgraph that contains v and doesn't contain any black vertex.
Now, let's see how the vertices change colour if we change the starting vertex from u to v, where u and v are neighbours. It turns out that only two vertices might change color: the vertex with the same label as u and the vertex with the same label as v.
If we had a data structure that supported the 3 following operations in (amortized?)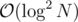 or better, then we would have a solution by DFS.
or better, then we would have a solution by DFS.
I have a solution in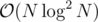 with HLD and lazy propagation. Maybe the operations can be somehow supported by centroid decomposition?
with HLD and lazy propagation. Maybe the operations can be somehow supported by centroid decomposition?