Help needed in a DP Optimisation Problem [SOLVED]

#	User	Rating
1	tourist	4009
2	jiangly	3821
3	Benq	3736
4	Radewoosh	3631
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3388
10	gamegame	3386

#	User	Contrib.
1	cry	164
1	maomao90	164
3	Um_nik	163
4	atcoder_official	161
5	-is-this-fft-	158
6	awoo	157
7	adamant	156
8	TheScrasse	154
8	nor	154
10	Dominater069	153

I've been stuck on this problem for a while (Lazy Cows USACO 2005 US Open Gold) . I was able to get the recurrence correct . But my naive approach (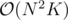 $\text{[math]}$ ) TLEs .

First I compressed the positions by sorting them based on their column and breaking ties using the row number

Then I pre-processed 3 arrays

costH1[i][j] stores minimum area covered using a single horizontal rectangle , from i^th smallest position to j^th . If it's not possible (cows are not entirely up or entirely down) then its INF.
costH2[i][j] stores minimum area covered using 2 horizontal rectangles . If it can be covered with a single rectangle then its INF.
costV[i][j] stores minimum area covered using a single vertical rectangle . To be more precise , its a rectangle with top left coordinate at (1 , coordinate[i]) and bottom right at (2 , coordinate[j])

Using these 3 arrays

DP[i][j] stores the minimum area covered by i rectangles for a prefix area till j^th column.

Base Case

DP[0][j] = INF

DP[1][j] = min(costV[0][j], costH1[0][j])

DP[i][0] = 0

My Submission : Commented Code

Can someone help me in optimising this recurrence relation.

Update

I would like to thank send_nodes for helping me in solving this problem .

AC CODE

Comments (16)

Write comment?

bhishma

7 years ago, # |

Auto comment: topic has been updated by bhishma (previous revision, new revision, compare).

→ Reply

send_nodes

As j increases, what happens to the value for k which attains the minimum?

7 years ago, # ^ |

I feel that they should increase , because cost[k][j] ≤ cost[k][j + 1] for a particular k . Also DP[i - 1][k] + cost[k + 1][j] ≤ DP[i - 1][k] + cost[k + 1][j + 1] for 0 ≤ k < j , so the minimum index increases as j increases .

Yeah, so you can use divide and conquer opt. to solve it.

Sorry I'm not aware of divide and conquer optimisation . Can you please explain it briefly .

So first, you should do an outer loop on i, and an inner loop on j to compute the DP (using your variable naming above). Naive way is O(N^2), but D&C can do it in O(N log N).

Idea is that if you want to compute dp[i][x] for all x in a range [l,r], and you know that the possible values for k (again using your naming above) lie in the range [a,b], you should compute dp[i][(l+r)/2] first and note the k that attained this minimum, let it be p. Then, you can compute dp[i][x] for all x in range [l,(l+r)/2 -1] now using the k-range [a,p] and dp[i][x] for all x in range [(l+r)/2 + 1, r] using k-range [p,b]. It works because of that monotonicity condition.

← Rev. 3 →

There is a problem . Our assumption that k increases as j is wrong .

For this test case (TC 6)

test case

99 99 1000000
2 996175
1 455803
1 106457
2 853751
2 350919
2 93554
1 370848
2 729954
2 208148
1 995614
2 266849
2 371154
1 182769
1 955896
1 953481
2 639955
1 481215
2 357189
1 960397
1 384241
1 940757
1 611567
1 73559
2 456762
1 425439
1 18079
1 259930
2 716839
2 545228
2 982075
2 367796
2 60587
1 400307
2 252461
1 590279
1 378630
1 69059
2 76316
2 711857
2 224041
2 856116
2 944737
1 971177
2 888292
2 895974
1 909431
2 968163
1 529298
2 568008
2 286496
2 419402
1 973155
1 320333
1 931978
1 723030
2 819983
2 922802
2 173244
1 232804
2 524303
1 873540
1 910819
1 860765
2 191697
1 668766
1 367308
1 128901
1 935999
1 912232
2 453139
1 72411
2 775086
1 788512
1 743317
2 460677
2 208368
2 253405
1 615001
2 646765
2 815352
1 405143
2 182679
2 982242
2 442221
1 891629
2 285833
2 141349
2 802125
1 881828
1 933439
2 887020
2 604946
1 83518
1 290272
1 780978
1 653588
2 524950
1 501947
2 91116

Using the naive approach the k array looks like this [-1, -1, 0, 2, 2, 1, 1, 6, 6, 8, 9, 8, 11, 11, 11 ... for i = 4.

What should I do now ?

Oops, you're right. Look at my comment below.

egj1996

In the second base case shouldn't it be: dp[1][j]=min(costV[0][j],costH1[0][j]) instead of i?

Thanks for the correction . I have updated it.

Ok, I finally managed to get this problem accepted. I used a different dp state:

(index, number of rectangles left to place, is there a horizontal rectangle ending at (1,index), is there a horizontal rectangle ending at (2,index), is there a vertical rectangle ending at (1,index) and (2,index) ).

It has N*K*2*2*2 states. For transitions, to get to some state, you can extend the top rectangle, extend the bottom rectangle, extend top and bottom rectangle, extend a vertical rectangle, create a new top rectangle, create a new bottom rectangle, create a top and a bottom rectangle, create a vertical rectangle, discontinue a top rectangle, discontinue a bottom rectangle, disc. a top and bottom rectangle, disc. a vertical rectangle.

Time complexity was O(N*K*(2^3)^2) for my solution. Cool problem, thanks for sharing :D

What do you mean by discontinuing a rectangle .

at index i - 1 we had some rectangle (top, bottom, top&bottom, or vertical), and at index i, we don't put any rectangle in its place (we don't create a new rectangle nor do we continue it). I guess better word is "ending" a rectangle.

Thanks a lot I was able to solve the problem.

bhishma's blog

Update