Is it possible to find MinCost MaxFlow if there is a negative cycle on the network?
For clarification: in this given network, each edge has unit capacity and the number denoted on each edge defines the cost. A is source and D is sink. In this network MaxFlow is 1 and MinCost is -3.
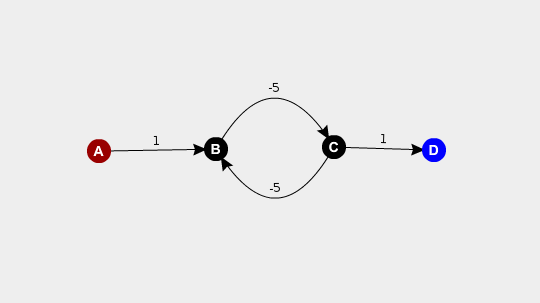
How to calculate the MinCost properly?










Answers to your questions are kinda yes and no simultaneously.
Yes, it is possible to find max flow min cost in that case. But no, standard MFMC don't do that in a sense that this is kinda separate problem. You need to modify your network before you use standard MFMC algorithms. You need to search for negative cycles as long as they exist and cancel them. Cost strictly decreases with every cancelled cycle, so you can't do that in infinity, but it doesn't seem to be a polynomial bound for time of this. Once you have network without negcycles, you can execute any MFMC algo.
If I'm not mistaken, when we cancel cycles with minimal average cost, it works in polynomial time. I remember some bounds like O((VE)^2 log(CV)) for integer case.
How do we cancel the cycles?
Find a negative cycle (well known problem, but a quite nasty one), find edge with lowest capacity c on it and let flow c units through it.