-emli-'s blog

AtCoder Regular Contest 076 / Beginner Contest 065
By -emli-, history, 7 years ago, In English

Two contests AtCoder Regular Contest 076 and AtCoder Beginner Contest 065 will be held at the same time.

You can participate in whichever contest you want. (However, you can't register to both competitions.) The last two tasks in ABC are the same as the first two tasks in ARC.

Time： June 24th (Saturday), 21:00 JST

Duration: 100 minutes

Number of Tasks: 4

writer： DEGwer

Rating： 0-2799 for ARC, 0-1199 for ABC The point value are:

ABC: 100 — 200 — 300 — 500

ARC: 300 — 500 — 700 — 1000

We are looking forward to your participation!

Let's discuss after the contest.

  • Vote: I like it
  • +47
  • Vote: I do not like it

Comments Comments (33)
| Write comment?
»
7 years ago, # |
← Rev. 3   Vote: I like it +30 Vote: I do not like it

I'm very impressed about writing ARC/ABC announcement every time without any skipping.

By the way, in June 10th, there was a contest in AtCoder that the writers are square1001 and I (E869120).
I really worried about the number of participants, but -emli- announced in codeforces 6 hours before the contest. So, the number of participant was 1165 (great value!), and the contest was successful.

I would like to thank you here. Thank you for -emli-, people who participated in AtCoder contests and everyone!

UPD: The ABC064 announcement is here, and the contest link is here.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +22 Vote: I do not like it

    Thank you ;)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      By the way, why "summer" "hot" are included the blog tags?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +15 Vote: I do not like it

        :) It's very hot in our city +30 and it was only joke.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +10 Vote: I do not like it

          Thank you, but in south pole, the temperature is under -50 degrees celsius. Too Coooooooold! (It is a joke)

          → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I coudn't have passed 20.txt in F :/

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

Sadness is when you get your solution on E correct 1 minutes after the contest.

Insert sad violin music

→ Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +26 Vote: I do not like it

I did it!
ARC 076

UPD: My rating decreased :(

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    I lost. My twin brother square1001 is making great records recently. Excellent!
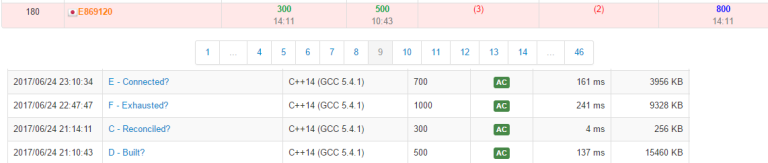
    By the way, I solved 2 problems in the contest, but I fixed bugs and finally I solved all problems of ARC after 31 minutes than contest ending without any editorials and advices.



    I think this contest is one of the most regretted contest for me (because I solved all problems in 131 minutes, but I solved only two problems in the contest).
    But I will devote myself to make use of the result next or in future.

    UPD: Though after the bad luck, finally, my contribution became to +106. Thank you for everyone.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +8 Vote: I do not like it

      Actually, in Atcoder, I had 19 losing streaks. So I really wanted to beat you! I mostly thought of beating E869120 in this contest. Might be I succeeded in listening your heart.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        Wow! You are twins. In childhood I dream have twin brother )

        → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Good luck :)
        I wish square1001 will be successful in future contest, but I'll devote myself to win him again.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

That feeling when instead of just going around the border I tried writing normal sweep line intersection algorithm ;-;

→ Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

This was my first contest at atcoder, the problems were cool :)

I don't understand something about the rating colors, why are there people in the top that aren't red (and by their rating they should)? xD

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    After some rating, you can apparently manually choose your colors. I don't have the link, but I am sure I read it somewhere.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    People with 3200+ rating can choose their own color.

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +13 Vote: I do not like it

    Top coders can change his color

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +15 Vote: I do not like it

      You said that rating 3200+ coders can change his color.
      It is right, but this described in a problem of AtCoder.

      AtCoder Beginner Contest 064 C- Colorful Leaderboard (Link)

      The problem's writer is I (E869120) and square1001, but make people know the AtCoder Rating Color System is one of the purpose to make this problem.

      → Reply
»
7 years ago, # |
  Vote: I like it +13 Vote: I do not like it

Lots of people solved F, but I wonder if everyone's deduction is similar to the one in the editorial, which seems to be quite complicated.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +52 Vote: I do not like it

    My solution is quite different (and it doesn't require any custom data structures).

    1. As 0 is a suitable point for all people, we can assume that all new chairs are there.

    2. It's clear that the function "Can we construct a perfect matching given X extra chairs?" is monotonic with respect to X.

    3. Let's use binary search. For a fixed value of X, we can process the people sorted by L[i] matching them to the smallest free position in their prefix if there is one and adding the smallest unused value of R among the processed people otherwise to a todo vector. After that, we just need to iterate over the todo vector and try to match it with the rest of the positions (we can do it greedily in linear time).

    4. The only data structure we need here is a priority queue for getting the smallest unused value of R.

    It might be pretty hard to prove the correctness of the step 3, but it seems more intuitive to me (and it also produces the matching explicitly, even though we don't need it here).

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +34 Vote: I do not like it

    I had yet another solution.

    Note that it only makes sense to match person i to a chair a ≥ R[i] and person j to a chair b ≤ L[i] if a > b; otherwise we can match i with b and j with a instead. Thus there will some number p, such that chairs a < p will only be mapped to people with L ≥ a and chairs a ≥ p will only be mapped to people with R ≤ a.

    If we know p in advance, the problem becomes a standard scheduling problem and can be solved greedily: Iterate over chairs from p - 1 to 1 and assign them to the person with greatest R among all available people (storing the R:s in a priority queue). Then solve the right part using the remaining R:s greedily in linear time.

    Treating one value p takes linearithmic time, so we need to avoid iterating over all possible values of p. Here I used a binary search: If we tried some value of p without matching all chairs from 1 to p - 1, then it makes no sense to increase p. Correspondingly, if we didn't match all chairs from p to m, it makes no sense to decrease p. (If we match all chairs, then we are done.) Thus we know whether to increase or decrease p next time, so using a binary search we only need to consider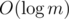 values of p.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +18 Vote: I do not like it

      You don't even need the binary search. You can simply find a solution that uses the most chairs from the left interval, and if you prefer people with larger R, you can then fill the chairs on the right greedily. Hence, you just do two simple scheduling problems.

      → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

for the problem E(Connected?), i got the idea that we have to check if any pair of line segments which have both the ends on the boundary of the rectangle intersect. I coded this using the link below.

http://www.geeksforgeeks.org/given-a-set-of-line-segments-find-if-any-two-segments-intersect/

My submission: http://arc076.contest.atcoder.jp/submissions/1379118

^ i have exactly implemented the algo given in the link. Please help me find the error.

EDIT: I found one error and still i get WA

Submission: http://arc076.contest.atcoder.jp/submissions/1379548

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Your code prints YES when the correct output is NO at the following test case:

    4 2 2
3 0 4 1
4 2 4 0
    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yeah i resolved that, thanks! but still i am getting WA. I changed the approach to check intersection to the stack-based one and i got AC. Now i am starting to think that the geeks for geeks article might be wrong.

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You are not solving the same task. You are connecting points by straight lines, and in this problem, curves are also allowed.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      The task reduces to this. See the editorial, we can prove that if the line segments which have both endpoints on boundary do not intersect, then a curve-drawing is always possible. This statement is iff.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Oh, my bad, I haven't noticed the part where you said you are only considering points on the edge.

        → Reply
»
7 years ago, # |
  Vote: I like it +23 Vote: I do not like it

In problem F, there are some ACs with incorrect greedy. We found a counterexample for these.

Code(writer: kriii): http://arc076.contest.atcoder.jp/submissions/1378411

4 10
1 3
2 10
2 10
2 10
→ Reply
»
7 years ago, # |
  Vote: I like it +18 Vote: I do not like it

For problem E can we do divide and conquer? First remove all useless lines which doesnt have its both ends on boundary. My idea was first choose a random line segment. And check if any other line segment intersects it(then NO). If not then that line segment divides the rest of lines into two different parts of line segments. Check for each part. To avoid anti quick sort examples do random shuffle once.

Is there any flaw in the approach since I m getting WA?

→ Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

What's the answer supposed to be for this case for Problem E (Connected?) ??

10 10 2
0 0 5 5
2 0 0 2
→ Reply