Hey, I recently managed to play with some small magnet balls and created a simple riddle:
https://www.dropbox.com/s/raleq3lsuhjr4pz/Riddle.mp4?dl=0

Question is: how many balls are there?
I didn't do anything sly, interior is filled as tight as it can be. Of course it is rather simple, but I find it entertaining. Please use 'hide' tags for answers.
UPD: Congratulations to lmn0x4F on being first one to give correct answer :)! If you want to read my explanation and additional comment then look at my answer to rng_58's comment.











I guess i'll try my luck, it's probably incorrect though XD
56
Yeah, you're right, it's incorrect =). This would be TooSimple ;p
Well you did say it was simple XD
Actually, thanks, that would have looked lame if first comment had contained correct answer :D
6*8 + 7 = 55
:p
That's right :). For a short explanation refer to rng_58's post
My very simple guess:
50
Compute the height, when radius = 2 the height is about 14.053!
UPD: There was a mistake, as the height of each layer I computed sqrt(4 - 1 / cos(15o)) instead of sqrt(4 - 1 / cos(15o)2), so it should be 13.978.
55.
Task: How many balls in
Michelangelo'sSwistakk's sculpture?How did you get that 14.053? Actually according to my calculations it is 13.978. Difference of height between two border layers is , so height of whole border is 2 + 7·1.7112 ≈ 13.978, so it should be a tiny bit shorter than column of balls in the middle.
, so height of whole border is 2 + 7·1.7112 ≈ 13.978, so it should be a tiny bit shorter than column of balls in the middle.
However when I looked closely it seemed that actually top middle ball is a little lower than top border balls. I think reason for that is same as why answer is not simply 56 meaning that center balls are not aligned to border balls. If they were perfectly on center then they would touch just two other center balls (one above it and one below), however these are magnets, so they have tendency to touch other border balls that are very close and because of that they misplace a bit from center and also lose a bit on height. However it is pretty tedious to take it into account in calculations, but definitely doable, Pythagorean formula is still enough.
May be
...54
...As there is not much space for all 8 balls to accommodate in center
I have a range
49-52
I think
8 * 7 - 1 = 55
Auto comment: topic has been updated by Swistakk (previous revision, new revision, compare).
By the way, it reminds me one of my favorite games in my babyhood.
I had lots of silver balls:
I also had Go's stones. I didn't use the stones in this game, I only used the lids:
Put n silver balls into the lid, stir them, and wait until they stop. Observe the pattern formed by the balls.
Formally, the surface of the lid can be approximated as z = k(x2 + y2), so we want to find (x1, y1), ..., (xn, yn) that minimizes the sum of xi2 + yi2 under the constraint that (xi - xj)2 + (yi - yj)2 ≥ 1. Guess what happens when n = 7. Can you guess the patterns for bigger n?
Actually, with surface equation as it is right now, minimizing potential energy is equivalent to minizing sum of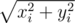 not xi2 + yi2, but I guess that answers don't change. Does the surface have shape of cone (current equation describes it) or paraboloid (what would correspond to minimizing sum of xi2 + yi2)? Moreover actual constraint is (xi - xj)2 + (yi - yj)2 + (zi - zj)2 ≥ 1, you forgot about z. Actually for n = 7 I have 3 possible candidates for answer, but it is hard to check which one is best, so I will just say that I bet on
not xi2 + yi2, but I guess that answers don't change. Does the surface have shape of cone (current equation describes it) or paraboloid (what would correspond to minimizing sum of xi2 + yi2)? Moreover actual constraint is (xi - xj)2 + (yi - yj)2 + (zi - zj)2 ≥ 1, you forgot about z. Actually for n = 7 I have 3 possible candidates for answer, but it is hard to check which one is best, so I will just say that I bet on
One ball in center and a ring of 6 balls on identical height that do not touch center ball.
Sorry it was like a very flat paraboloid. I guess this game is very boring for cones. k is very small and z term can be almost ignored (otherwise the pattern very heavily depends on the value of k).
Yes, for n = 7 you are correct, though I used to play it like 15-20 years ago and I can't confirm the answer for other n now.
If we ignore z term then this becomes very intuitive (however I am not sure how to prove this in two lines) and in fact all of my 3 candidates for answer collapse to the same one ;p.
I guess that for n ≥ 7 we can get a lot of different patterns as answers for a fixed n. Physics only guarantees to find a local minimum instead of global minimum and I think many "downward closed" patterns on triangular lattice can be local optimums.
Another example of geometric optimization problem where physics can help us that I saw was Steiner tree on a plane. Guy that was showing it had two glass tiles placed close and parallel to each other connected by short sticks in few places. He then sinked that in some soapish liquid and after taking it out that liquid created network of walls between these sticks that was sometimes a Steiner tree (and sometimes some other local minimum :P)
Would be funny to use physics to (NP-?)hard problems, however it seems that physics can only find local minimums and not global ones. And if there is only one local minimum then probably it can be found by local search/gradient descent or similar techniques?
Actually, physics can even solve problems harder than NP, so even if P=NP the quantum computation will be more effective than classical in some cases. An example that is already achieved by humans is boson sampling, that was done using integrated photonics. I know that some scientific teams try to use the same method for problems like finding exit from a maze.
I have also heard of a quantum computing circuit that can effectively simulate the dynamics of a particle, which is a computationally-heavy problem otherwise.
In physics, you usually use Monte Carlo method (a Marathon Match veteran would probably upgrade this to simulated annealing) to simulate the process of reaching equilibrium. If you take a bigger space (or even infinite and then talk about density of balls instead of their count) you may talk about phase transition. For counts/densities below threshold you will have mor or less chaos (i.e. liquid) while for higher densities you end up with order (i.e. solid).
The order may take various forms, e.g. triangle or square lattice. In finite case, there will probably be clusters of densely packed balls. In infinite case there should appear translational symmetry.
If the z-coordinate differences are small then it may be neglected in the radius condition and only taken into account as some potential energy that drives the balls off the edge.