gop2024's blog

Graph Theory Task
By gop2024, history, 7 years ago, translation, In English

Can anybody help me with this task: We have a tree with N verteces(N<=5*10^5). Each edge has got a length Li(Li<=1000). In each iteration we delete one(given) of un-deleted edges and we must tell the longest simple way in each of two resulting components and we doing it while all edges aren't deleted. Please, any ideas how to solve it?

  • Vote: I like it
  • +19
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been translated by gop2024 (original revision, translated revision, compare)

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by gop2024 (previous revision, new revision, compare).

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +11 Vote: I do not like it

First idea is to reverse the problem: instead of deleting edges we can look at the problem from the end and add edges.

Now all we need is to merge two trees into one and calculate diameter of a new tree. Consider trees T1 and T2 that are going to be connected by an edge (a, b), and let n(T1) ≤ n(T2). New diameter is the maximum of d(T1), d(T2) and 1 + d1(a) + d2(b), where d1(a) is the maximum distance from a to other vertex in T1, and d2(b) is defined in the same way for T2. Let's maintain these numbers after the merge: for T1 we recalculate all of values naively, using known d2(b). But for large T2 we can't do that. So let's remember that for every vertex x of T2 to find this distance in future we need to test its distance to a and relax this value by dist(x, a) + d1(a). Technically, it means that we add this condition for the whole component and iterate over vertices of T1 to cancel this condition for them. If the tree is merged then with larger tree, we throw away all these conditions. Because of that, we need to maintain only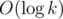 conditions for a component of size k. Because of that the whole algorithm works in .

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

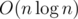    I dont understand, why we must maintain only O(logk) conditions?

    → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +42 Vote: I do not like it

    If we fix a diameter uv of some tree T and a vertex t then either u or v is the furthest vertex from t. Using this, for every component we just keep two ends of its diameter and update them accordingly, so I guess we just got significantly simpler solution.

    These contribute to resulting complexity: 1) computing O(n) distances, 2) find and union, so overall complexity would be . However if we want to get best theoretical complexity, to first one we can use well known LCA/RMQ thing in constant time per query and to second one if I'm not mistaken it is possible to do F&U in total linear time if we perform it on a planar graph that is known beforehand, so total complexity would be O(n), but you definitely do not want to code this like that ;p.

    Btw why is your solution in ? Did you already assume we can compute distances in O(1)? I think we are asking distance queries what when done in standard way takes

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Yes, you are right. Also my claim about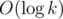 conditions is incorrect, it can be changed to if we rebuild all the stuff each steps. May be too much for this constraints, and your solution is much simpler.

      Btw, I think we can also solve this problem with centroid decomposition in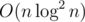 . The idea is to maintain for each subtree of centroids children the set (distance from centroid, last added edge on path), in which both coordinates are increasing. Then we can add subtrees one by one and relax the answer.

      → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Yes, it's simple and beautiful. Thank you very much

      → Reply