This time I've decided to play with spoilers to faciliate the presentation as some of the guys here did before. Tell me what you think about this write-up!
Problem A. Shifts
Topics: dynamic programming.
Summary: the first "hard" problem of the contest. Knowing your basic DP problems helps a lot, but coming up with the precisely correct solution may take a lot of persistence.
Solution: Suppose that we are allowed to make left circular shifts as well as right ones.
Problem B. Number as a gift
Topics: greedy.
Summary: a gatekeeper for inexperienced and/or impatient contestants. Many details to take into account, but otherwise tractable.
Solution: Since we aim to maximize the number, let us look what is the largest first digit we can possibly place. Let d denote the first digit of n.
Problem C. Recursive Generator
Topics: hashing/string algorithms.
Summary: while this is a simple problem, some approaches are better than others in terms of complexity, memory, and implementation tediousness. Pick your poison!
Solution: As a start, how can we prove why the Fibonacci sequence as described in the statement is not 1-recursive?
Problem D. Trading
Topics: greedy, sorting, implementation.
Summary: while the solution is not exactly evident from the start, one has to jumps a lot of hoops and dodge a lot of spikes to avoid all possible mistakes with precision, query limit and whatnot.
Solution:
This pretty much concludes the idea description.
Problem E. Manhattan Walk
Topics: maths, shortest paths in graphs.
Summary: even if you don't come up with a simple mathematical solution, graph algorithms save the day. Easy!
Solution:
Problem F. Tree Game
Topics: game theory, graphs, math.
Summary: frankly, I anticipated a lot more solutions on this problem. All ideas seemed basic to me, and the code is very easy. Still, it seems that cracking the whole thing was not that simple. Did you enjoy solving it? =)
Solution:
I'll be glad to hear all your opinions in the comments. Thanks for participating!



 in the sense that no character occurs more times in
in the sense that no character occurs more times in  time if we sort the tuples and compare only the adjacent pairs,
time if we sort the tuples and compare only the adjacent pairs, time if we hash the tuples beforehand using the
time if we hash the tuples beforehand using the 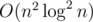 , or
, or  .
.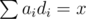 with high precision, and then make alterations to it so that the balance is decided on
with high precision, and then make alterations to it so that the balance is decided on 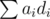 will be changed by the value of
will be changed by the value of 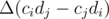 , which has the same sign as
, which has the same sign as 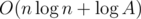 queries, in practice this number is about 450 on the present constraints.
queries, in practice this number is about 450 on the present constraints.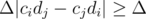 away from
away from 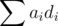 changes ever so slightly when add practically zero number to it, so that it can dance around
changes ever so slightly when add practically zero number to it, so that it can dance around 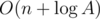 queries, where
queries, where 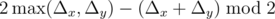 .
.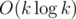 time.
time.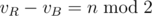 . It follows that the equivalent game would be to minimize
. It follows that the equivalent game would be to minimize 






D and (especially) F are great! Thanks.
Thank you for the great round. I enjoyed to solve A, very interesting problem:D
Let's define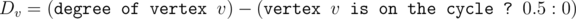 . Then the strategy "choose vertex with the lowest value of Dv among remaining vertices" is optimal. Is this correct?
. Then the strategy "choose vertex with the lowest value of Dv among remaining vertices" is optimal. Is this correct?
And I'll be surprised if the complexity is less than O(POLY·3V) in a general graph.
BTW, I was reminded of Euler Getter from F.
Yeah, looks good to me! I had something complex (and probably wrong), but now I see that this should work. I will probably leave the proof out for now though. =)
I stupidly used map<vector, int> in C and it passed in less than a second))
I also did it, but I don't consider it stupid ;p. However that's why I didn't submit it blindly because I was a little scared about getting TLE.
Why is binary search possible in problem C?
Suppose it is true for a certain length L that all different consecutive L-length tuples have different neighbours to their right(if they exist). I was not able to find any condition mathematically which could show for any length k (k>L), the given sequence is definitely k-recursive.
PS: I tried singe hashing first. It failed. Then I tried hashing with two primes and two big primes. It failed then too. The anti-hash tests were too strong. Can any one tell me which primes did they use for hashing? (in general also).
I think different consecutive L-length tuples arent necessary to have different neighbours to their right. Like a function having different parameter can give out the same value.
It is K-recursive if for every i, j that a[i — k... i — 1] = a[j — k... j — 1], a[i] = a[j].
Now assume It is K-recursive, then it is L-recursive (L >= k). Because first if a[i — k... i — 1] != a[j — k... j — 1], a[i — L... i — 1] != a[j — L... j — 1], so we dont have to consider them. If a[i — k... i — 1] = a[j — k... j — 1], now a[i] must equal a[j], so no matter a[i — L... i — 1] is equal to a[j — L... j — 1] or not, it is still valid.
This editorial is like Christopher Nolan movie. I keep peeling it and new layers keep coming up. At the end I am not sure if I understand the intended story :)
I hope I didn't go too far on the postmodern side in spite of clearness. Would you like something to be explained better?
It's nicely formatted editorial. I had some difficulty following the description for C. I don't understand the transition from Fibonacci series to "if there are two consecutive k-tuples of elements followed by different numbers, then the sequence is not k-recursive". e.g. 1,1,2,3,5,8 seems to match the given condition (1,1 and 2,3 is followed by 5,8) however it is 2-recursive. Source code accompanying the explanation would have been clearer for me.
Take random element, compare it with others and recurse to only one half instead of both (after determining which one). If elements less than this element already contribute at least x than we do not care about order of bigger elements.
Basically it's randomized k-th element algorithm.
Absolutely correct!
In fact it is also possible to adapt standard algorithm searching for median in deterministic way, that works the same way and ensures pessimistic linear complexity, however it would be more complicated to code (but we can make use of nth_element with custom comparator).
Pretty good problems and solutions both. Upvote without any hesitation. Problem A is very instructive to me to think more about LCS. However, I have some confusions about the contest rank. In the rules, it only tells that "Top 512 participants according to the cumulative result of all four elimination stage rounds will receive a contest T-shirt." But, what does the "cumulative results" mean? Does elimination stage show final rank? Sorry for disturbs:(
Yes, the rank is calculated according to the aggregated table at your link.
Here is my derivation for F:
Let's rewrite the score, for kR we can rewrite it as vR — eR; where vR is the number of vertices colored by Red and eR is the number of edges with vertices on both endpoints colored by Red.
Same for kB, we arrive at: (vR — eR) — (vB — eB) which is equal to: (vR — vB) — (eR — eB).
Firstly, observe that the term (vR — vB) is just a constant equal to n mod 2 as both Red and Blue take turns after each other.
Secondly, let's further rewrite the other term, we can observe that edges in the final graph are one of three types:
- eR, eB and eX: edges with different coloring of vertices on their endpoints. We'll rewrite eB as E — eR — eX, where E is the total number of edges. This results in the equation: n %2 — (eR — (E — eR — eX)), which we can simplify as: n %2 + (n -1) — (2*eR + eX).
Finally, we can observe that the last term: (2eR+eX) is exactly equal to the sum of degrees of vertices colored by Red, because, for each vertex colored by Red, all edges connected to it are either of type eR or eX, and edges of type eR are counted twice in the summation of degrees. Remember that the degree of a vertex in an undirected is the number of edges connected to it. So, the goal for Red or Blue becomes to minimize the sum of degrees of vertices colored by them, regardless of previous actions!
Consequently, the optimal choice for Red and Blue will be to color the minimum degree vertex that is uncolored. This results in Red choosing the vertices with the 1st, 3rd, 5th, 7th, 9th, ... (up to nth for odd n or (n-1)th for even n) minimum degree vertices, let's refer to the sum of degrees of these vertices as S.
The final score can be calculated directly as: n%2 + (n-1) — S.
S is calculated after taking the input and sorting vertices based on their degrees, this means complexty is O(n log n).