problem:
given at most 400 values of C. for each C,find an integer X (X<=10^18) such that 2^x mod (10^9 + 7) = c
i know that a value x must exist (X<10^9 + 7).but finding X is a problem for me. is there an efficient way to find x?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
problem:
given at most 400 values of C. for each C,find an integer X (X<=10^18) such that 2^x mod (10^9 + 7) = c
i know that a value x must exist (X<10^9 + 7).but finding X is a problem for me. is there an efficient way to find x?
| Name |
|---|



U can solve using shank baby step gaint step algorithm
To elaborate on teja349's answer, the idea is that there are at most m = 109 + 6 different values that 2x can take on, and if there is a solution to 2x = c, then you can write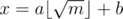 where
where 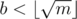 and
and 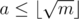 (modulo off-by-one errors).
(modulo off-by-one errors).
All you have to do is compute all possible 2x values where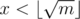 and throw them in a hashtable, and then for each value of a, check if there is some element in the hashtable having value
and throw them in a hashtable, and then for each value of a, check if there is some element in the hashtable having value 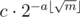 .
.