hrushikesht's blog

[SOLVED] Problem in understanding Magic Formulas(424C)
By hrushikesht, history, 7 years ago, In English

Hi,

I just read the editorial of Magic Formulas. I couldn't understand a particular formula in editorial.

In editorial it is written that,

.

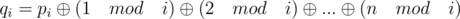But in question, the formula is given as,

.

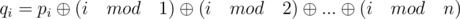I am not able to understand how these formulas are equivalent. Please help me understanding what I am missing here.

  • Vote: I like it
  • 0
  • Vote: I do not like it

»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Someone please help?

→ Reply
»
7 years ago, # |
  Vote: I like it +2 Vote: I do not like it

I don't know abt the editorial, but i will share my approach. let ANS denote final ans.

Firstly, we xor all the pi's — that's obvious, so ANS = (p1^p2^...^pn).

Now the problem is left to handle each of the i's form 1-N.

So, first we create a prefix xor of numbers from 1-N -> prefixXor[].

For 1 — the xor is always 0 as X%1=0 for all 1-N.

for the rest of the numbers, if (n/x) is even that means the xor's have been cancelled out and so we can xor our ANS with prefixXor[(n%i)], ans if(n/x) is odd we xor our ANS with (prefixXor[n%i+1],prefixXor[i-1]).

→ Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

The editorial is not saying the two expressions are equal it defines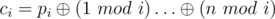 , which is different from the qi in the question. The trick is xoring all the ci together gives the same result as xoring all the qi together. If you expand the value of Q writing each qi on a separate line you can see the ci are the columns and the qi are the rows. So if you xor everything together you get the same result since xor is commutative. You are doing the same thing just in a different order.

→ Reply
»
7 years ago, # |
  Vote: I like it +1 Vote: I do not like it

hrushikesht Consider the formula of q_i and Q as given in the problem. Now expand the terms in Q by substituting values of each q_i. Now we know that 'xor' is associative so form a group of p_i with terms with (modi) and name it as c_i. And now the Q= c_1 xor c_2 xor ...

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by hrushikesht (previous revision, new revision, compare).

→ Reply