otero1991's blog

Geometry problem?
By otero1991, 12 years ago, In English

I wonder if somebody can help me to solve this problem: There is a set X of N point on the plane not two sharing the same x-coordinate, and a set Y of S points. The task is to compute for each point on X the distance to its closest point on Y with a precision of 10^-2 N,S<=10^5 and the coordinates of the points x,y <=10^6

UPD: Sorry for my English I corrected a mistake in the first line

  • Vote: I like it
  • +3
  • Vote: I do not like it

Comments Comments (3)
| Write comment?
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

http://en.wikipedia.org/wiki/Delaunay_triangulation NLogN with any precision

→ Reply
»
12 years ago, # |
← Rev. 2   Vote: I like it +8 Vote: I do not like it

You can use the following heuristics: choose a random line and project all points on it. Then, for each point X, move two pointers in the both directions and stop a one when |posX - posY| >  = Ans, where the expression under modulo is distance between projections of X and some current point Y and Ans is the best answer for the X at this moment.

This algo is easy to implement and it works good in average, but fails on a special test cases (something like 'a lot of points on a circle'). I've heard that it works in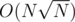 in the 'find two nearest points' problem.

You can also take a look at the Codechef's CLOSEST problem and its editorial.

→ Reply
  • »
    »
    12 years ago, # ^ |
    ← Rev. 2   Vote: I like it +8 Vote: I do not like it

    but fails on a special test cases (something like ‘a lot of points on a circle’)

    The test is: X = points on the large circle (coordinates are rounded to integers), Y = points near the center of the circle

    it works in O(NsqrtN) in the ‘find two nearest points’ problem.

    It's true even for more complicated problem, in case X = Y (for each point from X find the nearest one from Y).

    → Reply