Codechef May challenge has ended.
Let's discuss problems
Why answer will be 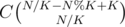 for SANDWICH ?
for SANDWICH ?
And how to solve KILLER?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 155 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Codechef May challenge has ended.
Let's discuss problems
Why answer will be 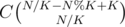 for SANDWICH ?
for SANDWICH ?
And how to solve KILLER?
| Name |
|---|



Auto comment: topic has been translated by CMaster (original revision, translated revision, compare)
The minimum number of sandwiches is . Suppose we give K to each of them. We have used
. Suppose we give K to each of them. We have used  too many meters of sandwich. We have to take out a bit from some sandwiches in such a way that it sums up to what we need to erase.
too many meters of sandwich. We have to take out a bit from some sandwiches in such a way that it sums up to what we need to erase.
Recall that the number of ways to write N as a sum of K non-negative numbers, where order matters is . You can prove this by bijection.
. You can prove this by bijection.
Combine these observations and you end up with an equivalent formula for the problem.
It says in the problem statement that we have to find this value mod P. When P is prime, we can find it by using Lucas Theorem. But how will we solve it when P is a composite number? (I know it involves Chinese Remainder Theorem but I think I'm missing something.)
We need to find some C(N, K) modulo M. We can factorize M into different P^q and use Chinese Remainder Theorem to find an answer.
Now, our aim is to find C(N, K) modulo some P^q. How to do that? First of all, let's try to use formula N! / (N — K)! / K!. But we can't divide as (N — K)! and K! are not co-primes with P^q. We can actually compute factorials without P's and calculate degree of P in C(N, K) afterwards.
So, what does the factorial without P mean? Pseudo-code is here:
Let's call this factorial N!!.
Then C(N, K) mod P^q is N!! / K!! / (N-K)!! * P^k, where k is degree of P in C(N, K). As K!! and (N-K)!! both aren't divisible by P, they are coprimes with modulo and we can easily divide by multiplying to inverse numbers.
Last step is finding out how to calculate N!!. Let's have a look what N!! is: 1) First, we multiply all numbers which are not divisible by P. 2) Let's have a look at multiplies of P. They are P, 2P, 3P, ..., floor(N / P) * P. After dividing by P, these numbers become 1, 2, 3, ..., floor(N/ P) and we can solve recursively.
Finally: N!! = (N / P)!! * multiplication_of_numbers_which_are_not_divisible_by_P mod P^q.
Second part is easily calculated in O(P^q).
Thanks a lot!
f[0] = 1; for (int i = 1; i <= (p^q); i++) { int x = i; while (x mod P == 0) x /= P; f[i] = (f[i-1] * x) mod P^q. }
now N!! = (f[p^q] ^ (N / p^q)) * f[N % p^q] mod p^q.
Is it wrong?
Yes, it is wrong. For example, N = 6, p = 2, q = 2 , then 6!! = 45 = 1(mod 4), but f[4] * f[2] = 3.
Thanks :)
First we know that the maximum number of groups will be [Ceil], which actually will consist of (floor)
[Ceil], which actually will consist of (floor)  partitions with value = K and one partition with value N%K. Now we can see that we can not decrease the the size of partition N%K, because then we'll have to increase the size of other partitions which will violate the conditions. Now we can increase the size of this one partition from N%K to K, which means we are getting some values from the other partitions. So, We can increment it's size from 0 to (K - N%K). That means we have to find the non-negative integrals solutions of this equation t1 + t2 + ... + tx = Δsize where X = floor
partitions with value = K and one partition with value N%K. Now we can see that we can not decrease the the size of partition N%K, because then we'll have to increase the size of other partitions which will violate the conditions. Now we can increase the size of this one partition from N%K to K, which means we are getting some values from the other partitions. So, We can increment it's size from 0 to (K - N%K). That means we have to find the non-negative integrals solutions of this equation t1 + t2 + ... + tx = Δsize where X = floor  and Δsize is from 0 to (K - N%K). So for a particular Δsize our answer is
and Δsize is from 0 to (K - N%K). So for a particular Δsize our answer is  .
.  . Now, write
. Now, write  . If we combine this term with
. If we combine this term with  , we get
, we get  . Now combine this with other terms, you will finally get
. Now combine this with other terms, you will finally get  . [Note : We have combined two terms using the property
. [Note : We have combined two terms using the property  ]
]
Now we have to find summation over all the Δsize. Let us denote R = K - (N%K). Now we have to find sum of this value
Hi!
Can someone please explain the following solution for the KILLER problem? Thanks!
https://www.codechef.com/viewsolution/13623489
I also still don't know how to solve this problem. I'm especially curious why does chemthan's solution work. I know a similar trick called "LiChao segment tree", but I don't see why does it work for parabolas too (the trick by default is for line functions). If someone knows can he/she explain. Thanks in advance.
The key: Two functions have at most one common point.
Thanks. I actually didn't notice that.
If you don't mind, can you please explain the approach? Thanks!
If you know convex hull trick for equations of the form of a straight line, you can extend it to parabolas.