Hi everyone.
I'm trying to solve this problem 559B - Equivalent Strings but I'm getting TLE here's my submission 26805388.
Now let's calculate the time complexity of this solution one call of function "is_equal" is O(n) in complexity because of the "substr" function which is linear in complexity.
Now for how many times we will call function "is_equal"...it should be O(log(n)) because each time we are halving the strings so the numbers of times I can do that is log(n) right ?
So the total time complexity should be O(NlogN) right ??? why am I getting TLE is there anything that I'm missing ??? I will be grateful for any help.
Thank you for reading.
:)











You call your function 4 times each recursive call in worst case. What makes you think it's logN complexity?
Assuming each time your N gets halved this gives you logN depth but the number of sub problems is 4 to the power of something. ( Level i has 4^i subproblems). I think it's summation of powers of 4 from 0 till logN, something along these lines.
In binary search you only branch to one sub problem, here you branch to 4 instead so you can't use the same reasoning.
Hope that helps!
Nope, complexity is O(n2) in your case. Your solution makes much more than calls (at the very least it makes O(n) calls because
calls (at the very least it makes O(n) calls because
is_equalcan be called from any substring of length 1).If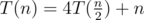 . It can be solved using master theorem: T(n) = O(n2).
. It can be solved using master theorem: T(n) = O(n2).
is_equalis called from two substrings of lengthneach, then it makes approximately n operations by itself and callsis_equalrecursively four times, passing strings of lengthn/2each time. If we denote total running time ofis_equalas T(n) (herenis length of the arguments), then we get the following recurrence: