Hi everyone!
Baltic Olympiad in Informatics is being held in Bergen, Norway. Here is the official competition site.
I am wondering — will there be any online mirror? It would be great if there actually was one, it doesn't seem probable :/
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 165 |
| 3 | Um_nik | 161 |
| 3 | atcoder_official | 161 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
Hi everyone!
Baltic Olympiad in Informatics is being held in Bergen, Norway. Here is the official competition site.
I am wondering — will there be any online mirror? It would be great if there actually was one, it doesn't seem probable :/
| Название |
|---|



Seems like you can register in https://boi17-open.kattis.com/ provided in the official website.
How do you find the list of Kattis mirrors like these? For example, naipc17.kattis.com, etc? I've searched kattis but there's no list of these subdomains.
sorry but i found the website in the official boi webisite > <. But I think searching site:kattis.com naipc17 or boi17 or other contest in google can find the result
BOI is held on Kattis this year, that's why there even is a Kattis mirror.
Also, the public ranking of an onsite contest will be available here: https://boi17-public.kattis.com/
Can please someone share solutions?
Problem 3
Build a virtual tree for every query(using those node and their lca) . Then compute partial sum on tree. After all query check if the edge is >= k.
Can you please share more details? I don't understand your idea.
As sigma(si) < = 2e5. We now have to add 1 to every edge which between those si nodes. Notice that the path is the union of a[i] -> lca(a[i], a[i + 1]) -> a[i + 1] if we sort a by their in order time. But some path might intersect. So we can build a tree only consist of a and their lca. We then travel the node of the tree and do partial sum on tree (we build and travel for every query). As sigma(node size) <= 2 * sigma(s_i), it is enough.
For how to build a virtual tree, you can take a look at https://blog.sengxian.com/algorithms/virtual-tree which is the blog written by sengxian (cool blog). Although it is in Chinese there are pictures and codes so it is easy to understand too.
I know my English and presentation is just awful. You can take a look of my code http://ideone.com/fFIXFT
Thank you.
Sort them by dfs traversal order. Add 1 to all path from vj — v(j + 1)modsi is enough. This adds all edge value in "virtual tree" by 2
I feel very troll now :'(
I guess you add 1 using prefix sums?
w prefix sum + lca
But how does this work on the right side? In DFS order to the left you have straight chains so you can do prefix sums. But when you go right, there are paths to the left between "straight chains", so more connections are counted (as necessary).
Yes. And in fact, it is counted exactly twice. So there's no difference.
When you must output the edges, how do you know which are counted due to right prefix sum?
Ah now I realize your point. That's why I separate path s — e to s — lca(s, e) — e. This separation yields two path to root, which you called as "straight chains".
I don't understand something. Let's say s is in left subtree of LCA(s, e) and e is in right subtree of LCA(s, e). Adding s is not problem. But I can't find an efficient way to add only chain to the right. Can you share your code, please. Maybe this will help.
Now I don't realize what you are curious for... whatever, this is my AC code, as you requested.
https://github.com/koosaga/olympiad/blob/master/Baltic/baltic17_railway.cpp
Thank you very much. I understand now. I thought you did cnt[i] += cnt[i — 1] according to DFS traversal array, not another DFS. That clarifies everything.
How to solve A ???
:)
For given graph, there exists some node which have smallest degree.
So, we find that node, and calculate all clique containing that node (in 2^k time). After that, we should calculate all clique that "does not" contain such node, which can be done by simply removing that node.
How do you find cliques containing that node in O(2^k)?
We know there must exists a node X with at most K neighbors. We'll find the one with minimum number of neighbors (so, at most K). Now, if we want a clique containing the node X, its members are limited to X and X's neighbors. Now, you can choose the subset of neighbors of X that are contained in the clique and check if they really form a clique. In my source, I've reindexed the nodes with numbers from 1 to K + 1 and remembered for each pair whether there is an edge or not. To do it, I just used a set, but it generally work with any hash (hence, K^2logM or K^2 time complexity for each iteration, but it's negligible compared to 2^K)
Thanks a lot. Could you please briefly tell the solution to the second task?
First, divide nodes of the original graph into N/K groups so that node number I belongs to the group I/N. Now we can define a single node X by its group number X/K and X mod K. As a preprocessing we store T[g][m1][m2][i] which denotes minimum distance from node which belongs to group g, is m1 modulo K to node in group g + 2^i, which is m2 modulo K. We can calculate this table by simple for loops. When we receive a query we can simply change nodes a,b to their groups g1, g2 and rests m1, m2, and then iterate through all bits of number g2 — g1 (jump pointers) in order to perform a simple "dp", we simply move number g1 to the right by powers of 2 contained by number g2-g1 and calculate our partial result (res[x] table which denotes distance from node a to current jump with modulo K equal to x) based on previous "jumps". After the iteration we print res[m2]. Time and memory complexity is something like N*K^2*logN.
Correct me if I'm wrong, but I understood, that it's sufficient to apply such algorithm: 1) Select a vertex with min degree, remove it from the graph, reduce all its neighbours degree by 1 and put them in priority queue 2) Try all subsets of its neighbours to form maximal clique (as you've mentioned, the complexity of such process is 2^K, where K doesn't exceed 10? (or what?)(why does it always hold, as total neighbours count can be N-1?) And what's the overall complexity of yours solution? Is it N * 2^K?
You understood it right.
Total neighbor count can be N-1, but you selected a vertex with min degree, and there always exists some vertex with deg <= K (Because, by statements, such vertex always exists in any subgraph), So trying all subsets are sufficient.
My complexity is N * 2^k * k^2
Will there be an online mirror for the second day?
No, really, will there be an online mirror for day 2? Cause' it's about to start.
yes, same link: https://boi17-open.kattis.com/
Anyone else having login problems?
Can't register for an account. :(
Sorry, registration is not open.Is there a solution easier (to write) than centroid decomposition with a segment tree for 6th problem?
Apparently this problem is a weaker version of this Atcoder problem.
yes it is. I wrote just simple linear dp and it passes.
in each node I remember two values:
the distance to the nearest cat already marked
the distance to the farthest node on which we can still put a cat
Can you elaborate a bit? I've had an idea of another DP, but a much more complicated one. Your idea seems too simple.
here is a (not so neat) code: https://pastebin.com/XuCnE25D
The idea : we replace each subtree by a path of len <= d/2 such that the answer will not change.
Suppose that our current node is v and we want to replace its subtree by a path. And we already replaced childs subtrees by some paths. If all those paths are shorter than < d / 2 then we leave only the longest path.
If there are paths of length d / 2 then we put a cat at the bottom of such paths and delete this part from the tree. (be careful when d is odd).
6 5 0 1 2 3 0
Your program outputs 1, answer is 2.
yep. Still it gets 100 at kattis.
I guess the issue is with the condition at the end when we finally reach the root we sometimes should add 1 to the answer...
Tests for p6 seems pretty weak (my n^2 testing code unexpectedly got AC)
Just greedily pick node farthest from root. If we pick that node we flood fill from that node.
Let Depi = distance from node 0. We still greedily paint the node. For node i, if there is some node j s.t Depi + Depj - 2 * DepLCA(i, j) < D, then we can't paint that node.
Answer is at most O(N/D). Consider euler tour of tree. If two selected node are closer than D in euler tree index, their distance is always less than D. This property is useful because we can afford D operation for every selected node.
For node v, maintain closej = (minimum depth of selected node in j's subtree) - 2 * Depj. If there is some node j in parent of i, with Depi + closej < D, then we can't paint it. otherwise, we can paint it.
If we paint that node, we should update closej. However, we can afford D operation here. So we iterate through it's D ancestor, and update closej.
We do all above operation in O(lgN) time with segment tree. So (O(N) + O(N/D) * O(D)) * O(lgN) = O(NlgN)
Code
However I think there are simpler solution than this.
Can you give a proof that picking farthest node is optimal?
2 years later, and I still don't know why picking the furthest node is optimal :((
7 years later, and I still don't know why picking the furthest node is optimal :((
Let's say you pick nodes in nonincreasing order of depth (once you pick a node, you can't pick any node in its subtree). Imagine you don't pick the furthest node. Then you instead of picking that node you can pick one of that node's children. You are guaranteed to not pick any less nodes, but there is a chance you can pick extra nodes this way.
Can please someone share solutions of second day?
for B just observe that there are two types of possible boards:
A[i, j] = ( - 1)xi + j for some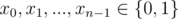
A[i, j] = ( - 1)i + yj for some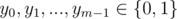
and each constraint gives us the values of xi, yj
So answer is only 0, 1, 2? Or do I have to do some kind of DP?
Let us look at the possible boards of the first type. There are two possibilities:
constraints are inconsistent for example one gives x1 = 1 and the other x1 = 0. in that case there are no solutions.
there are k different constaints. In that case there are 2n - k possibilities.
Do the same for the second type. And be careful because there are two colorings (usual chessboard) which are of the both types.
A: Solution sketch (I didn't implement the solution, though):
I'm sorry to revive the topic. Although the contest is over, but does someone know whether it will be possible to submit solutions for Day 1 contest? Because it appears, that only submitting problems for Day 2 is available at the moment, or am I missing something?
Is there any way to submit solutions now? The Kattis contest is dead.
UPD: Apparently not...