Given a binary tree,
We have to remove a single edge and partition the tree into two new trees such that difference of their diameters remains less than a given constant k.
Please suggest me an approach of O(n) time complexity.
| # | User | Rating |
|---|---|---|
| 1 | jiangly | 3976 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3482 |
| 8 | hos.lyric | 3382 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3357 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 168 |
| 2 | -is-this-fft- | 165 |
| 3 | atcoder_official | 161 |
| 3 | Um_nik | 161 |
| 5 | djm03178 | 157 |
| 6 | Dominater069 | 156 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 9 | awoo | 151 |
| 10 | TheScrasse | 147 |
Given a binary tree,
We have to remove a single edge and partition the tree into two new trees such that difference of their diameters remains less than a given constant k.
Please suggest me an approach of O(n) time complexity.
| Name |
|---|



Auto comment: topic has been updated by go_rob (previous revision, new revision, compare).
one way is to store the three longest paths starting at each vertex (note that each path should go through a distinct vertex), this can be done in O(N) and having this information you could easily choose an edge to remove and compute the diameter of each tree.
I found a method but I don't think it is the best approach. It seems too messy for my taste — I would like to hear any better solutions!
First find diameter of the tree using any standard method — let its endpoints be d1 and d2. Notice that if d1 and d2 are the in the same partition, that is the worst case scenario, as it will have the original diameter (i.e. partitioning did not improve diameter). So let's suppose d1 and d2 are in different partitions.
Therefore, we must remove one of the edges on the path between d1 and d2 to disconnect them. Let's consider the whole diameter path. Let it be d1, a1, a2, ..., ak, d2. Notice that d1 and d2 have degree one. Also notice that all nodes "a1, a2... ak" have only one edge not on the path, because binary trees have max degree 3.
We can precompute value of prefix and suffix easily then. For each of "a1, ..., ak", we consider the subtree contained by the 'extra' edge (we proved earlier that there is only one such edge). We also compute the maximum depth within this subtree. With this information we can compute diameter of a "prefix" or "suffix" of the array. Then we can simply try removing each edge and using precomputation to get minimum result, which is enough to answer the question (if the minimum is better than k, use that result; otherwise, it is impossible).
I am not sure about my solution, but looks reasonable to me.
----------------------spoiler-------------------------
so say u have a binary tree looks like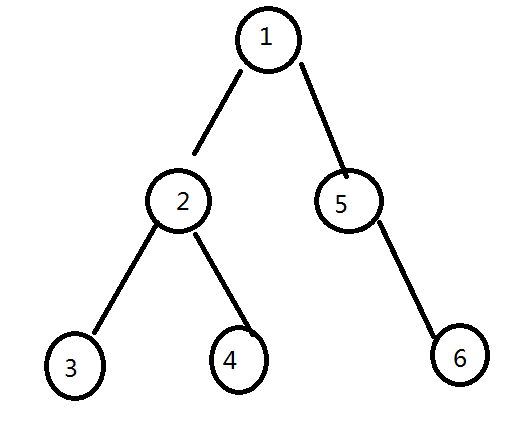
let f[i] represent the longest distance from i to any vertex in the subtree of i.
it is easy to get in o(n).
so consider we are deleting the edge from x to its father. (in the figure we assume x = 2)
therefore the tree is split into two parts, rooted by 2 and 1.
for 2, the diameter = f[lson]+f[rson]+1 (coz it is binary tree)
for 1, the diameter = f[rson]+1
so u can just bruteforce the deleted edge, and calculate the difference.
I think it is reasonable for me, but if there is something wrong or bug, please point it out, thanks a lot.
Your solution seems buggy.
The two Eqn for the diameter that you have written doesn't hold true for many cases.
ah sorry i misread the problem,
so like, u make dp[i] to the diameter of the tree rooted by i.
the same thing, then for 2, it looks like dp[2] straightly. for 1, it is max(dp[rson], f[rson]+1)
is it work? sorry for the retarded previous answer :L
I don't think your solution will work in all cases. The max(dp[rson], f[rson] + 1) will not not always work.
I am providing a better solution here
Guys, I have found out a solution using DP which will work in O(n) using 2 DFS. Here is the code, Please check the code and verify its correctness.