Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
Tutorial is loading...
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3857 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3463 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 4 | atcoder_official | 158 |
| 6 | Qingyu | 156 |
| 7 | djm03178 | 151 |
| 7 | adamant | 151 |
| 7 | luogu_official | 151 |
| 10 | awoo | 146 |
| Name |
|---|



ответ жюри 0, тогда как q = 0 и в массиве нет числа 0? Или я чего-то не понимаю?
Все вопрос отпал(
kak eta?
I can't agree more,the 14th test case should “inf” for output,but answer was '0'.why ????????
Stops writing when dx>l, so when trying to write d1 this is met and stops.
maybe there was a argument for this problem!
I did Div 2 C using another method for final iteration.
I sorted the skip array by their absolute value. So, the array will look something like this
2 -4 5 8 -8 10.Then, in the progression loop, I use a pointer which points to the next element of skip array. I increment the pointer until
abs(skip[pointer])>abs(elem). Then, check ifskip[pointer]==elem.I think div2 C, D and E are really nice problems
simple solution of div2C/div1A..http://ideone.com/SCmlJ2 using dp without pointer..
Can someone please explain how the graph is constructed in Div 2 E and why it helps in finding the solution of the problem?
I submitted some wonky solution for C which works in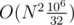 . Couldn't prove a tighter bound myself but it runs pretty fast.
. Couldn't prove a tighter bound myself but it runs pretty fast.
Did anybody else do the same? Could you prove a tighter runtime?
The idea is that the more unique drinks you have the lower your total volume required
I got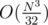 , I did the same, that you, but remembered on i-th iteration only dp positions from i·n - 1500 to i·n + 1500. Didn't prove it too.
, I did the same, that you, but remembered on i-th iteration only dp positions from i·n - 1500 to i·n + 1500. Didn't prove it too.
I did something similar, but I proved that the answer, if it exists, is bounded by 1000. Imagine that we have two sodas with concentrations X and Y such that X ≤ N ≤ Y. If this is not the case, then the answer is clearly - 1.
If it is, then we can use a mixture with N - X liters of soda Y, and Y - N liters of soda X. The total number of liters is (N - X) + (Y - N) = Y - X, and the total units of carbonation is (N - X) * Y + (Y - N) * X, which simplifies to N * (Y - X). So there is always an answer using Y - X liters, which is worst case 1000.
Yes, the answer bounded by 1000, for this 1000 iterations 3000 operations over bitset of size 3000, it leads to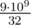 (at least my solution)
(at least my solution)
25922518
After some thinking I found that the max number of vertices (and bitset size) can be reduced to 1001, or more precisely, max si - min si. So it can be O(109 / 32) in total. The following is the proof. [Somewhat longer than socketnaut's elegant proof for another factor "1000" :) ]
According to the Editorial, "the problem is to find a set of numbers with zero sum" from s1 - n, s2 - n, ..., sm - n. Note that the vertices represent the "partial sums". Let's prove that if we sum up these numbers by a specific order, then all the partial sums will be within [min si - n, max si - n]. If this is true, we will only need to store at most 1001 partial sums.
Let ai = si - n, amax = max si - n, amin = min si - n. Obviously, the partial sum of only one number p1 satisfies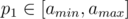 . We will prove that for all k, the partial sum
. We will prove that for all k, the partial sum 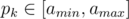 , using a specific summation order.
, using a specific summation order.
So each time we will add one number ak to the current partial sum pk to get pk + 1 using this rule: (1) If pk < 0, then select one ak from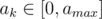 . Such ak must exist because otherwise the final total sum will never become 0, which means no solution. (2) If pk > 0, then select one ak from
. Such ak must exist because otherwise the final total sum will never become 0, which means no solution. (2) If pk > 0, then select one ak from 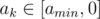 . Such ak must exist, too.
. Such ak must exist, too.
Using mathematical induction. Assume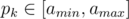 .
.
Now if we want pk + 1 > amax, we must have added a positive ak. Then we must have used rule (1). From rule (1),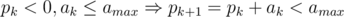 . So it is impossible that pk + 1 > amax. Similarly, it is impossible to get pk + 1 < amin.
. So it is impossible that pk + 1 > amax. Similarly, it is impossible to get pk + 1 < amin.
The "rule" is just a proof and we do not need to fix that in the code. 25941854.
Often the easiest of proofs seem wonderful. Although intuitively I felt that the answer should be bounded by 1000, I could not come up with a proof. This helped a lot. Thanks.
I simplified the equation to:
(a — n) * x + (b — n) * y + (c — n) * z = 0
(for concentrations a, b, c and x, y, z liters used respectively).
Then I did a BFS to solve this, bounding the total sum between -10**6 and 10**6 and transitioning by 1 liter of any particular concentration for every state.
I thought this should be O(10**6 * 10**3) but it passed under 1 second somehow?
Is this weak testcases or is my solution faster?
Submission: http://codeforces.me/contest/788/submission/25943628
The intuitive hand wavy proof for this is that the more different concentrations we have the fewer steps are required to construct the target sum. Two co-primes will require 1000 or so steps, but your BFS will perform quickly because of the low number of new nodes at each step. Each new option will reduce the minimum step count somewhat significantly.
Unfortunately I didn't have
ios::sync_with_stdio(false); cin.tie(0);in my code and it TLE'd while reading input... :(In problem Div1 D, there is no need to randomize. First I find, as explained in editorial, all points x such that there is a line (vertical or horizontal) that pass through (x, x). Then, to test if the line is horizontal or vertical (or both) I pick some y such that certainly no line pass through (y, y) and query the points (x, y) and (y, x). f(x, y) = = 0 iff there is a vertical line in x, because we know there is not horizontal line in y, the same idea apply to f(y, x).
My submission here. 25933644
I used a different (and I think simpler) approach for Div1E.
Start with the same pre-processing as in the editorial, computing smaller_prefi and smaller_sufi for all i. Once we've done this we can forget about the assistants and concern ourselves only with ways to select the three players.
For each distinct skill value v, create a separate segment tree to count possible teams such that the players have skill v. The segment tree for skill value v should have one leaf for each soldier with skill v.
In the segment tree nodes we put 4-by-4 matrices m, where mi, j indicates the number of ways to select players [i, j) from that segment. So for someone unable to play we should set his leaf to
and for someone able to play we set
Node combination is simply defined as matrix multiplication, and checking m0, 3 in the root for the segment tree for skill value v tells us the number of teams that may be formed with players having skill v. To handle queries we just need to change the leaf associated with the enabled/disabled player, and update the total according to how the root of the modified tree changed.
The complexity is the same as the editorial,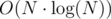 at the beginning,
at the beginning, 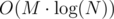 for handling queries, and O(N) memory for the segment trees.
for handling queries, and O(N) memory for the segment trees.
I solved Div 2. C using very basic Kadane's algorithm. Used two arrays A1 and A2 to store the absolute difference of the adjacent elements of the actual sequence.Then changed the signs of values at odd positions in A1 and values at even postions in A2. Then used Kadane's algorithm to calculate the maximum subarray sum in both the sequences. The maximum of the two is the answer. Here is my solution. http://ideone.com/K75Mu4
I did exactly the same xD
I had trouble transforming the usual Kadane's algorithm into one that could update the current maximum value considering the actual element just when it was an odd/even position correctly.
http://codeforces.me/contest/789/submission/25925332
It's really chaotic, but the same idea xD
I still can not believe that this algorithm has a name
In Div2 C in the first sample :
5
1 4 2 3 1
How is the answer 3 for the range [2,5] because i am getting -3
|4-2|*(-1)^1 + |2-3|*(-1)^1 + |3-1|*(-1)^1 = -2 + 1 — 2 = -3
Solved :
I got it i thought the equation had (-1)^(i-1) but infact it was (-1)^(i-L) i think the image should be clearly given.
For Div2 E, Div1 C: "Obviously, we'll have at most 1001 different concentrations, so there are at most 1001 edges from each vertex.". I coudn't get it, can someone prove or explain this statement?
Even though k can be upto 10^6, each ai can only be from 0 to 1000. We don't care about bottles with the same concentration and can ignore them. Hence there can only be 1001 (0 to 1000 inclusive) distinct bottles.
Now I see, thank you very much!!
it is first time i met prob with number and graph combined !! Thanks for nice prob !
It would be better if div-2 problem C was problem B. Problem B was not that hard but problem C was far more easy. Almost everyone knows how to find the maximum subarray sum using kadane's algorithm.
In Div1 B , I inserted all the nodes present in the edges in set to find the total number of nodes visited every time . And , for this my solution got TLE . I know I could do it in linear time , but I dont understand why it should get TLE . Link below .
http://codeforces.me/contest/788/submission/25916059
In problem C, why is "We need at most 1000 vertexes to each side (from -1000 to 1000)" true? Can't the value intermediately overflow 1000 and then decrease to n
Suppose the final set of values we select is v1, v2, ....vm. We know that their sum is 0 and they are in the range [-1000, 1000]. We start from sum=0 and pick them one by one and increment sum, till none are remaining. This is same as rearranging them in an array such that sum of every prefix is also in that range. We choose items in order from left to right. We keep track of current sum. If it is >=0, we choose any negative value among the remaining (which we haven't used yet), else use any positive. This will ensure that at all times, the sum always remains in that range and we eventually reach 0.
div2 C why do we have to make two arrays with +,-. Could not find logical error in my code.where am i wrong?
my code
Isn't this submission O(10^9)? Why does it pass?
div2 B (789B - Маша и геометрическая депрессия)
I'm failing to understand the reasoning behind this in the tutorial:
Specifically, I think that test 45 (25944979) contradicts the problem description.
My reasoning:
I appeal to the problem description:
So, we must skip b1 and move to b2 regardless of |b1| value if b1 is "bad".
What am I missing?
In other words, why in Div2 B answer=0 in test 45?
2,0,0,0,...
2 is bad, 0 is good, L=1
I think we must skip 2 without comparing it against L because 2 is bad (according to the problem statement). Which leads us to answer=inf.
It's clearly written in the problem statement that "Masha writes numbers while condition |bi|<=l", but here b1 is 2 which is greater than l(here 1) . So he can't write any numbers on the board.
In Div1 C, how we can make the graph ? I think there can be n^2 vertices and n edges connected to every vertex. I think it needs n^3 memory.
Hi, could someone please give a more detailed explanation of the idea behind Div2D/Div1B? Especialy the translation to finding a Euler path and regular edges. Also what does we "split into 2" mean?
I would be very grateful since i can solve Div2 A,B,C in contests for some time now, but can never come to understand D.
In Div2 D, for adding the number of pairs with loops, should we not be adding loop.(m-1) instead of loop.(n-1)? For each loop we select we pair it with any of the (m-1) edges, isn't it?
Thank you, fixed.
In 788B
Regular(not loops) edges that are not adjacent — graph has four vertexes with odd degree, so Euler path doesn't exist.
if two regular edges are not adjacent, our graph can also have two vertexes with odd degree. how to prove the answer is right?
Can you construct such a graph?
like a square? opposite edges ? and each has degree 2?
Note that non-chosen edges are doubled in the problem solution. So, when you do it in the square graph you'll have all vertexes of degree 3, that is 4 vertexes of odd degree.
Can anyone please tell what difference would it make if multiple edges are allowed in problem 789 D / 788 B ?
For Div2 E, why does it reduce to subset sum = 0 ? Aren't we allowed to choose any no of liters of a particular concentration? If a1,a2,...,am are the distinct given concentrations, and x1,x2,...xm denote the amount in liters taken from each type. We want to minimize x1+x2+...+xm
sigma(xi*ai) = n*(x1+x2+....+xm)
=> x1*(n-a1) + x2*(n-a2) + ... + xm*(n-am) = 0
What i dont understand is that why xi = 0 or 1 ?
x1 * (n — a1) is treated as x1 different sodas each with concentration (n — a1).
Then how can we claim that m is atmost 1001?
http://codeforces.me/blog/entry/51312?#comment-351961
http://codeforces.me/blog/entry/51312?#comment-351976
xi is not 0 or 1, eg in the second sample case itself, xi = {1,3}
I can't understand Div2 E, why 1000 vertexes to each side (from -1000 to 1000) ??
I understand why the answer must be bound under 1000 but why do there can be atmost 2001*(min(k,1001)) iterations that will run????..wont it be greater than it??..I mean its gonna check for all posiible combinations for which a particular number 'x' comes through sum of different numbers if we keep the structure of the graph in mind...
hi
in problem div2 C i use to <bits/stdc++.h> library but i got wrong answer and bellow error on test 4
Can't find file C:\Contesters\Work\invoker-prod\work\codeforces2\46035c1543108537f31faf5ce95ef250\check-81db4cd701e94f7f6059055741b7386c\run\output.fd0138e687.txt.
when i changed library into iostream i got accepted
can someone explain why? and when i can use from <bits/stdc++.h> library?
Can someone explain how build final graph in div1C?
i think test case 18 for D has some bug... someone please confirm