Let's discuss problems.
Does anyone have an idea for D?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3856 |
| 2 | jiangly | 3747 |
| 3 | orzdevinwang | 3706 |
| 4 | jqdai0815 | 3682 |
| 5 | ksun48 | 3591 |
| 6 | gamegame | 3477 |
| 7 | Benq | 3468 |
| 8 | Radewoosh | 3462 |
| 9 | ecnerwala | 3451 |
| 10 | heuristica | 3431 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 167 |
| 2 | -is-this-fft- | 162 |
| 3 | Dominater069 | 160 |
| 4 | Um_nik | 158 |
| 5 | atcoder_official | 156 |
| 6 | Qingyu | 153 |
| 7 | djm03178 | 152 |
| 7 | adamant | 152 |
| 9 | luogu_official | 150 |
| 10 | awoo | 147 |
Let's discuss problems.
Does anyone have an idea for D?
| Name |
|---|



How to solve C, H, G, K?
H: The answer is the number of ways we can delete two vertices from the tree so that the size of its maximum matching doesn't change.
Compute this by subtree dp: dp[x][u][k][r] is the number of ways to delete r vertices from the subtree of x such that the size of its maximum matching is k smaller than the size of the optimal matching for the subtree of x. If u = 0 then x is not matched and not removed (we can later match it to its parent) and if u = 1 then x is removed or used in the matching.
You should count each way of removing vertices only once, so you should fix a strategy to get exactly one maximum matching for each set of removed vertices. One way to do this is to match a vertex to its first child that is not matched or removed.
C: First, I put vertex on each edge. [v1-v2] => [v1-e1-v2] So, this problem can be solved with dominator tree, but I get TLE. So, I rewrite program more faster, faster, faster...., I get AC with 0.999s/1s!!!!(with +14...XD)
H: If we know edmond's blossom algorithm, we can convert this problem to "we have forest those vertex colored with red, blue, yellow. count (u, v) with color(u) == red && color(v) == red && path(u, v) have blue vertex." Construct forest and solve this problem are easy, but my poor english can't explain this convert...
G: choose a root arbitrarily(respecting all the requests), then recursively solve for each connected component of "i want this guy to be my superior"-requests.
Wow. before reading your solution I thought my algorithm was wrong. but....
I am very suprised it was solved by just 7 teams. It was meant to be one of easier problems. On AE it was solved by ~75 people including some Div2 guys.
Some of this desperated div2 guys like me spent 24 hours on the problem on AE ;)
C : We will disregard all vertices which is not reachable from 1.
We calculate DP[i] in topological order, which is
For some vertex v
It's not hard to prove why this works. O(n+m)
K. Sort the array a. For each i we want to check whether we can distinguish ai and ai + 1. We can distinguish them if there exist x, y such that
We define dpL[i][j]: the minimum z such that z%C = j and z is the sum of some subset of the first i elements. Similarly define dpR for suffixes. With these DP arrays straightforward checking of the conditions above will work in O(NC2). It's not hard to improve it to O(NClogC) with priority_queue.
Why should we check only ai and ai + 1?
We get 2N numbers by measuring all subsets. These numbers can be divided into two multisets of size 2N - 1 by the inclusion of particular item. We can't distinguish two items when this division results in the same pair of multisets, thus this is an equivalence relation.
Why is this true? We also know which elements were for every number in multiset.
Upd.: I understand why this is true: a_i is equivalent to a_j if for every subset of {1..n}/{i}/{j} we get the same value. So I got solution using two iterators for 2*n * nc.
Upd.2: I proved it from my understanding but still don't understand your prove.
Suppose that the multiset corresponding to the subsets with a1 (call it X) and the multiset corresponding to the subsets with a2 (call it Y) are the same. In this case, the multiset corresponding to the subsets that contain a1 and doesn't contain a2 (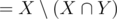 ) and the multiset corresponding to the subsets that contain a2 and doesn't contain a1 (
) and the multiset corresponding to the subsets that contain a2 and doesn't contain a1 (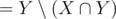 ) are the same. In each of these sets, obviously the numbers are sorted by the part that comes from {a3, ..., aN}, so for any subset S of {a3, ..., aN}, the "weight" (shown by the scale) of
) are the same. In each of these sets, obviously the numbers are sorted by the part that comes from {a3, ..., aN}, so for any subset S of {a3, ..., aN}, the "weight" (shown by the scale) of 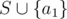 and the weight of
and the weight of 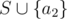 are the same. That means even if someone secretly swaps a1 and a2, you can't notice that.
are the same. That means even if someone secretly swaps a1 and a2, you can't notice that.
Yes, this proof is easier than mine. Thanks.)
"For each i we want to check whether we can distinguish ai and ai + 1" — omg, that's so trivial and brilliant and the same time :o
We can improve it to O(NC) by using sliding window with deque.
C. We've got a topological sort of the graph vertices, sorted edges by the left edge vertex according to the topological sort and processed edges. Let's call the vertex that can be reached by two necessary paths "good". Let's process the edge A -> B. If B has not been visited earlier, remember its parent A. Otherwise find LCA(A, parent[B]) and check whether there is the good vertex on the path between LCA(A, parent[B]) and A or between LCA(A, parent[B]) and parent[B] or not. If there is such vertex on either of these paths we call the vertex B "good".
H:Calculate maximum matching bottom-up. For each matching edge color black the parent side vertex of it (all other vertices are white). Cut edges connecting two black vertices. For each black leaf remove it and adjacent white vertex. Remove black vertices has at least three neighbours. Then, we can connect two vertices if and only if they are white vertices from different connected components.
Problem D:
If you sort (ai,bi) by ai, then you need to do this: take maximum element and change all numbers to the right b_j+=a_j (its own adding value) and delete maximum (put -inf). We couldn't understand how to implement it.
Where can we find results?
http://opencup.ru/
Explain, please, samples in problems I and O(div 2).
How to solve O,E div2?
Some ideas for D:
Sorry for posting completely wrong stuff
The problem is pretty similar to Bear and Bowling from one of Errichto's rounds. You can write the DP and optimize with f.ex. splay. You can also write a not-very-nice segtree or sqrt convex hulls (the last thing actually worked for a nonzero number of points of AE, but it's really unlikely to squeeze it for accepted)
Problem A please!
Probably the easiest way: create a trie containing all the binary words describing the correct assignments of the variables x1, x2, ..., xn (e.g. if the assignment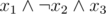 is okay, we want the trie to contain the word 101). Do it using the following construction: start with a single leaf (no variables). Add the variables in the decreasing index order.
is okay, we want the trie to contain the word 101). Do it using the following construction: start with a single leaf (no variables). Add the variables in the decreasing index order.
When adding a variable xj to the trie T describing the choices on variables xj + 1, ..., xn, we need to take two copies of T and join them with the root (for each possible choice of xj). Then, for each clause starting with xj, remove the appropriate subtree from the trie (e.g. if the clause if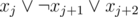 , remove the subtree 010 as it fails this clause).
, remove the subtree 010 as it fails this clause).
Doing it straightforwardly, we'd have an O(2n + m) algorithm (m — total length of the clauses). However, instead of copying the tries, we can make them persistent and get the linear runtime.
In other words, we need to count number of binary words so that it doesn't contain any of forbidden substrings (for every substring we have one particular place it is forbidden).
Let's assume we fixed some prefix of our word. Key observation is that how it affects our future choices is only through smallest i such that there exists a forbidden substring starting at position i that so far matches our choices. So we can use dp that for every such state will keep number of such prefixes. Number of such states is total length of forbidden substrings. We need to cleverly create a dp for position k + 1 if we already know dp for position k. What we need to solve is following problem "Assume we are in state S. What will be state if we append 0/1 to the end?". You can answer that if you keep states in some clever tree structure (maybe it has some clever name like KMP automaton or Aho, I don't know).
Can you please explain the last part (appending 0/1 and finding new states after that) in more detail?
During the contest we came up with everything except this moment.
Fix position k. Let s1, ..., sl be forbidden substrings that contain position k. We consider their prefixes not further than k-th position — call them r1, ..., rl.
We say that ri is descendant of rj iff rj is suffix of ri. We say that ri is child of rj is ri is descendant of rj and there is no rk such that it is in between (meaning it is descendant of rj and ri is descendant of rk). You can see that everything is well defined and we get some tree structure on those strings. Another way of getting it is considering trie created from reversed strings ri and marking their ends in that trie and compressing it so that we are left only with nodes that are marked.
Let fix some particular node in that tree (that corresponds to some ri). Assume its next symbol is 0. Then if we append 0 we go to state corresponding to same string. If we append 1 we need to go to some strings that is our ancestor. Out of those we need to chose the longest one so that its next symbol is 1. These can be determined by running simple dfs that goes from top to bottom and keeps arrays of two elements meaning what is the lowest node that is my ancestor and is extended by appending 0/1. When doing this we need to keep track of whether some string that is our ancestor will end if we append 0/1 in which case there is no next state for corresponding transition.
Here is my code, I think it is pretty clear: http://ideone.com/psR3HF
Full solution to D:
We observe first three observations that Lewin noted. Using this we arrive at what -XraY- said. Unfortunately, I don't know any way it can be implemented in an efficient way (Marcin_smu do you know one? I didn't get whether that's what you do).
We assume glades are sorted according to ai. Let p1, ..., pn be optimal order of adding glades to our partial solutions (that means, if we want to get answer for k days we need to collect mushrooms from glades of indices p1, ..., pk in an ascending order of a values).
We need to turn our thinking upside down. Instead of determining firstly p1, then p2 and so on for each k we will determine optimal order if we consider only glades with k smallest ai values. Key observation here is that adding $k+1$th glade doesn't affect order of adding previous glades (what follows from what -XraY- said)! So $k+1$th order will be $k$th order with $k+1$th glade inserted somewhere in the middle. Given this we can determine those orders using your favorite balanced binary tree.
By the way, I think that third Lewin's claim is highly nontrivial. My proof used some augmenting paths-like argument, but I don't remember it now clearly.
I like that problem very much, it's sad nobody solved it, but I am not very surprised since it took me 5 hours to come up with solution and 5 hours to code :P (this was my first time I implemented BBST). However on AE ~10 people got full marks (but we were given almost 2 days), so it was not impossible to solve it.
I think I have very easy proof of this fact.
Suppose i0 is the item with the biggest bi (if there are many of them, we choose arbitrarily). I claim, that we should take this item at some moment for each k. It's easy: if we don't take it, then we can change our first move and take i0 as our first move.
Also, it's trivial, that for each k we should take items in increasing order of ai (because we can swap two adjacent items in our sequence). And we know, that we should certainly take item i0. So, if we just delete item i0 and for every item i such that ai > ai0 we increase bi by ai, then we get the same problem as before.
Ahh, yeah, that's nice :).
The Lewin's idea can be implemented in time n^3/2, but such complexity of course don't get accepted.
How to solve B?
First, consider table dp[i][j] — minimum cost to transform first i symbols of pattern into first j symbols of text. We have dp[0][j] = 0(because substring can start at any position) and usual transitions.
Now for each difference j - i(say j - i = d) and each value s(0 ≤ s ≤ k) let's find the maximum i such that dp[i][i + d] = s, call it f[s][d]. If one of these maximums is equal to |P|, then we found a required substring.
f[0][d] is just equal to lcp of P and T[d..] To calculate f[i][d] it's enough to consider f[i - 1][d + { - 1, 0, 1}], skip one symbol in P, T or them both, move forward by corresponding lcp and choose maximum of three values.
Our solution for C:
Main idea is to track "sources" of single paths to quickly check whether different incoming edges to this vertex are from the same "source".
Lets associate with every graph vertex two additional values:
paths[i]is amount of paths that lead to vertex with numberifrom vertex1.0 <= paths[i] <= 2. Initiallypaths[i] = 0for everyi > 1andpaths[1] = 2source[i]is the pointer to the vertex from where single path that leads to vertexitakes it's "source". (only matters for vertexes that has it'spathsset to1)"Source" of the path is the vertex with
paths=1and there is an edge that leads from vertex withpaths=2to this vertex.Algorithm:
Lets calculate
pathsfor each vertex in thier topological order.Calculating for vertex
i: lets check every edge that leads to vertexiwhether this edge give us additional path to this vertex. Lets calljthe vertex that is the start of current edge that leads toi.If
paths[i] == 0 && paths[j] > 0then we can add path fromjtoiand setpaths[i] = 1. Now we should set the "source" of this path: ifpaths[j] == 2then we create new "source" of single path that starts in vertexi, ifpaths[j] == 1then we "push the stream" from some other "source" and save the pointer to it's initial "source" —source[i] = source[j]If
paths[i] == 1then we can only accept another path form another "source" or from the vertex withpaths[j] == 2If
paths[i] == 2already then we cannot change anything and we can skip all other edges to this vertexIn the end just print all indexes of
2inpathsarray.Complexity: O(N+M)
Why does it work: Sources of single is just an end of edge from 2 paths to one: they path spread thier "single stream" to all edges that can be reached from this source and all of them will point to this "source". All the vertexes that can be reached only through this source use edge that created this source — all of them become unreachable if we remove this edge. If the vertex can be reached form multiple sources (or directly of two-pathed vertexes with two edges) it becomes two-pathed itself and can create this own sources. Two-pathed vertexes can create infinite new sources because we need to make only two path and in the end to answer we can choose two for each vertex and find answer.
Probably this is the easiest solution to implement: only topological sort is required. And solution code is also pretty short.
What do you think about this?
Where I can find the statements?
Problem E?