DeshiBasara's blog

ICM Technex 2017 and Codeforces Round #400 (Div. 1 + Div. 2, combined) Editorial
By DeshiBasara, 8 years ago, In English
Tutorial is loading...
Code
Tutorial is loading...
Code
Tutorial is loading...
Code
Tutorial is loading...
Code
Tutorial is loading...
Code
Tutorial is loading...
Code
Tutorial is loading...
Code
  • Vote: I like it
  • +61
  • Vote: I do not like it

Comments Comments (29)
| Write comment?
»
8 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Can someone explain me the C Molly's chemical value. What would be the time complexity of the solution?

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 2   Vote: I like it +1 Vote: I do not like it

    O(log(base(k)[(10^14)])*log(n)*n)

    Explanation:- 1. distinct power of K => log(base(k)[(10^14)]) 2. total distinct sum= total maximum distict cumulative sum is n , as we are using map for the search total searching complexity for required sum is log(n). 3. and array size is n . - See solution : Solution Link

    → Reply
»
8 years ago, # |
  Vote: I like it +26 Vote: I do not like it

I want to share an alternative solution to Problem D which uses 2-SAT. Let p and q be the switches of a door. If the door is locked (equal to 0) you need to get it to 1 applying p or q, this the same as doing . Similarly if the door is unlocked (equal to 1) you should do 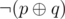(because you want that the door doesn't change).

Then you should transform each of this expressions so that you get a conjunctive normal form, you can do it like this:

And now for each door you have one of this expressions and you can do 2-SAT with this.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    And then you can see that when you added 1 one-way edge, you also added its reverse as well thus you can easily solve this problem using disjoint set.

    → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -8 Vote: I do not like it

    Beautiful solution!

    → Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    wow

    → Reply
»
8 years ago, # |
  Vote: I like it -11 Vote: I do not like it

Можно пожалуйста вопрос про D. Предположим мы ходим по графу и разукрашиваем его, допустим текущая вершина покрашена в цвет 1. Далее мы продолжаем его разукрашивать, и каким-то образом идем по ребру веса 1 в эту же вершину и цвет не совпадает, мы сразу выводим "NO". Но разве мы не можем пойти по какому-нибудь другому пути, где их цвета совпадут? Почему это работает ?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Если ты покрасишь 1 вершину в один цвет, то есть только один способ покрасить оставшиеся вершины. Ты ходишь по вершинам и разукрашиваешь их. Если ты смог покрасить весь граф по выше описанному алгоритму, то ответ есть, иначе если ты не модешь разукрастить граф, то ответа не существует. Подумай над этим.

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

can you check my account? 2 problems were accepted but my rating don't change!

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Your submissions were skipped because someone has the same code as you. Did you use ideone.com or other online IDEs? If yes, many people had a chance to copy-paste your solution(cheaters)

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      oh no, I give my code to my friends :|

      → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

For problem C, using unordered_map gives TLE on test case 101, whereas it gives AC using maps. Aren't unorderd_maps supposed to give better runtime or is this because of the rehash or something ?

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Because of collisions unordered_map works with complexity O(n) in worst case while worst case for simple map is O(logN)

    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

776C — Molly's Chemicals why unordered_map cause TLE?

I just replace unordered_map with map.

AC code : http://codeforces.me/contest/776/submission/24956397
TLE code : http://codeforces.me/contest/776/submission/24956380

can someone tell me why? please.

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Problem D
Can someone please help me debug this code
The approach was following:
1. Find controlling switches for every room and join them with edge weight 0 if room is open else with edge weight 1.

2. If room is open it means sum of toggling times of switches controlling it, should be even,therefore edge of weight 0 is added and vice-versa. (Edges therefore denotes parity of sum of toggling times to open this room.)

3. After the graph is constructed look for an odd-weighted cycle in the graph.

4. Existence of an odd-weighted cycle would mean there are two different paritys of sum of toggling times of same pair of switches , which is not acceptable ,Hence ans is "No"

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone please explain the dictionary part in problem C.

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    You don't have to watch at every prefix before current position, with dictionary you can easy find number of required sums with log(n). Otherwise u will get TL, cause of O(log(10^14)*n^2)

    → Reply
»
8 years ago, # |
  Vote: I like it +3 Vote: I do not like it

I dont undertand Problem C at all.How are we distinguishing whether we are getting subarray sum or subset sum?How are we making sure we are taking subsegment.I just dont get it. Please someone help and clarify in Laymen terms.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 5   Vote: I like it -8 Vote: I do not like it

    I also don't understand the method described in editorial, but I can tell about my solution =)

    Let's say we have an array A = [2, 2, 2]. The total number of different subarrays looks like that (I will write all of them as pairs of indices [start, end]):
    [0, 0], [0, 1], [0, 2],  Subarrays starting with 0
         [1, 1], [1, 2],  Subarrays starting with 1
              [2, 2]. Subarrays starting with 2

    In total there are 3 + 2 + 1 = 3 × (3 + 1) / 2 = 6 different subarrays. For an array of size n there are n × (n + 1) / 2 subarrays — too much to handle them one by one. That is why we split them cleverly into groups.
    As you can see from the picture above there are 3 different groups of subarrays. I will call the group of segments that starts with index 0 as group0 = {[0, 0], [0, 1], [0, 2]}. The group of segments starting with index 1 as group1 and the last group with a single subarray as group2.

    Why should we split them like that? This will allow us to reuse calculations for the first group0 in the other groups in the following order:
    group0 ⟶ group1 ⟶ group2

    That is, we first calculate the sums for all of the subarrays in the group0 directly without any clever manipulations like that:

    int A[3] = { 2, 2, 2 };
int group_0_sums[3] = { 0, 0, 0 };

group_0_sums[0] = A[0];
group_0_sums[1] = A[1] + group_0_sums[0];
group_0_sums[2] = A[2] + group_0_sums[1];

    Now I will place these sums in a map<>, because we need to count how many times a certain sum has appeared among subarrays in group0: 

    map<int, int> cnt;
for (int i = 0; i <= 2; i++)
  cnt[group_0_sums[i]]++;

    And now we are ready to reuse them in group1. First thing that we know is that in the best case, even if all of the sums of subarrays in group1 will match our requirements (powers of k) the number of subarrays in group1 is smaller than in group0 by 1 (number of subarrays in group0 is 3 and number of subarrays in group1 is 2). That is why we have to get rid of one of the subarrays in cnt[].

    What subarray sum we need to get rid of? That is subarray [0, 0], because it doesn't intersect with any of the subarrays in group1:

    cnt[group_0_sums[0]]--; // Get rid of subarray [0, 0].

    Now cnt contains sums of the 2 subarrays: [0, 1] and [0, 2]. But they start at 0, so we cannot reuse them as if they are subarrays of group1...
    But we can notice one thing if we put remaining subarrays of group0 with subarrays of group1 in front of each other:
    group0: [0, 1], [0, 1, 2]
    group1:   [1],   [1, 2]

    You see? They differ only in one thing: subarrays of goup0 include the element A[0], but subarrays of group1 are without it! So we can reuse all of the sums in cnt by shifting the value that we want to look up by A[0]. For example, if we want to check how many subarrays from group1 have a sum = 4 we will do the following: 

    int shift = A[0];
int needed_sum = 4;

int subarrays_with_sum = cnt[needed_sum + shift];
    → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

Problem C Molly's Chemicals can be solved using divide & conquer: 24957185

First we compute prefix sum in O(N)

Divide the array into half, until it has 1 element left. We try to recursively find the desired segment sums from left half and right half (The segment TOTALLY fall into those half)

For conquer part, we add up the return value from left half, right half, and those segments which cross the middle line, which can be calculated as follows:

  1. Let A[i] & A[i+1] be the elements across the middle line. Use O(N) to find all segment sums which segment end at A[i], named it LEFT. Similarly, use O(N) to find those starts with A[i+1], named it RIGHT
  2. Use O(N lg N) to sort RIGHT. Then for each LEFT, for each K power, binary search RIGHT to find if there is a number which can add up to the number. This step use O(N*K*lg N)

Together we got T(N) = T(N/2) + O(NK lg N)

I tend to see K as a constant, so I think T(N) ~ O(N lg^2 N)

→ Reply
»
8 years ago, # |
  Vote: I like it +2 Vote: I do not like it

In question C, can anyone please explain the author's solution..

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone help me find my mistake for Div2/D. I am solving it using 2-SAT and getting WA on test 24 25295970

→ Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why doesn't author give a link https://en.wikipedia.org/wiki/Euler%27s_totient_function ?

→ Reply
»
5 years ago, # |
  Vote: I like it -8 Vote: I do not like it

Wow, problem D is a bad problem

→ Reply
»
22 months ago, # |
  Vote: I like it 0 Vote: I do not like it

wow

→ Reply