Siriuslight's blog

Can this problem be solved using segment tree?
By Siriuslight, history, 8 years ago, In English

Can this problem problem be solved using segment tree. If yes can anyone can tell how to build Seg tree.

During combining two segments how do i check for mid and (mid+1)th element in merged segement.

  • Vote: I like it
  • +6
  • Vote: I do not like it

»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Auto comment: topic has been updated by Siriuslight (previous revision, new revision, compare).

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

It can be solved by Mo s algorithm using map to store count in O(n sqrt(n))(if we use unordered map)

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    We can just simply store the frequencies of numbers with int[] as the numbers greater than n can be omitted.

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Ohh nice idea. but how do u choose block size because every time block size sqrt(n) won't work sometimes 2*sqrt(n) will work instead. How to decide on block size

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Umm... for the problems with n = 105, I usually take SIZE = 300 just for simplicity.

        And I have never faced that Mo's Algorithm is one of the intended solution but it cannot pass just because my SIZE is not good enough. Can you share the cases that sqrt(n) cannot work properly?

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          check these submissions of mine

          1.here size= sqrt(n), time limit exceeded(5000 ms)
          2. here size= 3/2 * sqrt(n),time = 4180 ms.
          3. here size= 2*sqrt(n), time = 3086 ms.

          → Reply
          • »
            »
            »
            »
            »
            »
            8 years ago, # ^ |
            ← Rev. 2   Vote: I like it 0 Vote: I do not like it

            [Sorry, just ignore this]

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              8 years ago, # ^ |
                Vote: I like it +1 Vote: I do not like it

              How does that matter .Arent both same
              returning a.l<b.l is same as query1.left / SIZE < query2.left / SIZE when both are not equal isnt it?

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                  Vote: I like it +3 Vote: I do not like it

                Here, check this out — http://codeforces.me/contest/86/submission/24900658.

                This is the submission which TLed. Use this comparison in future. I don't know why it works better, I saw it somewhere. I believe it was in UnknownNooby's comment but not sure.

                → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                8 years ago, # ^ |
                ← Rev. 3   Vote: I like it 0 Vote: I do not like it

                Since P_Nyagolov summoned me, I'll try to explain this. First of all, this is still not the best comparison, I'm no longer exactly this, I'm using better one:

                Long story short: keep block number inside of your structure and compare these values instead of calculating blocck every time, make it so that in all even blocks a.r ≤ b.r, and in all odd blocks a.r ≥ b.r

                When you are sorting you will compare your values times, due to this you will divide times, which can be actually way slower than 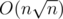simple operations. This way you speedup the std::sort called before Mo's.

                Second optimization which is that I reverse all even blocks makes the Mo's itself run faster on average. Think of it this way: when you finish performing operations on a block, if next block isn't reversed, you will firstly have to delete most of elements just to handle first query of a block, though it would have been easier to compute later queries first because their right border is closer. On random testcases this is a huge leap in perfomance.

                → Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it -8 Vote: I do not like it

read editorial editorial

see implementation source

implementation uses Fibbonachi Tree, but it easy converted to segment tree if you want.

→ Reply
»
8 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

P_Nyagolov Wow .It is such a good heuristic .
It almost reduces the constant in the running time by half.

And I think it can be easily justified. In previous version for each block we are moving from left to right and then again back to leftmost to begin for the next block (this last step for moving back takes O(n) time).
In the version u mentioned if for a block if we travel from left to right then next block from right to left (in this case we are avoiding that O(n))
That O(n) is now avoided for sqrt(n) block transitions.so we are saving a total of O(nsqrt(n)) time out of total time (which i feel will be 2*N*sqrt(N) to 3*N*sqrt(N) by taking all things into consideration with very less approximation).
So now we have reduced running time almost by 1/2.

→ Reply