If you are a contestant, you can be relaxed and you can do anything (except for cheating). It's perfectly fine if you just guess the solution and submit it without knowing why (though personally I don't find it very beautiful). However, if you are a writer, you need to prove your solution. Here is the list of things you have to prove:
1. Correctness.
Does your solution always return correct answers for all possible valid inputs?
- GOOD: Strict proof.
- BAD: My intuition tells that this is correct!
- BAD: I tried really hard to come up with counterexamples, but I couldn't. It must be correct!
2. Time Complexity.
Does your solution always run in time for all possible valid inputs?
- GOOD: It's O(n2) and the constraints say n ≤ 1000. It should work.
- GOOD: For this problem we can prove that the slowest case is xxx. Experimentally, my solution works for the input xxx under the given TL.
- BAD: I tried really hard to generate various testcases, and my solution passed all cases!
3. Randomized Algorithms.
Randomized algorithms are not hackish ways of solving problems. The writers should prove that for any valid input, the intended solution works correctly with very high probability. Please check here for an example of such proof. Another example is Rolling Hash: please check here. Note that, for example when we compute 105 hashes for strings of lengths 105, you need four hashes of prime modulo around 109, not two. (Practically two works but we can't prove that).
4. Precision.
Especially in geometry problems, we sometimes use epsilons. However writers should be careful about the use of epsilons.
- GOOD: We know |b| and |d| are up to 104. Let's use eps = 10 - 9 for comparing two fractions a / b and c / d.
- BAD: Let's use eps = 10 - 9! (without reasons)
When the intended solution uses complicated double operations (like sqrt, trigonometry, log, lots of fractions, etc.) such analysis may be hard. In this case, one possible way is to add constraints like "even if we move a point by up to 10 - 3, the answer doesn't change".
For the section 1 and 2,
Is it good that you can't prove that the solution works correct and steadily fast for every possible scenario (ex. whole positive integers), but you can test every possible data under the problem's constraints (ex. the input is an integer between 1 and 1,000,000,000 and you can test all of them) and it works correctly?
In the past Codeforces problem, you have to assume Goldbach's conjecture is correct if the integer is smaller than 4*10^18 to solve, and that was a little controversial. What if you can test every possible cases (since it's not clear which case is the slowest) working efficiently fast but don't know why?
I don't really see a reason it wouldn't be okay.
Checking every single possible case is a valid proof. (e.g. Four Color Theorem) If you tried every possible case and the slowest one is xxx, that constitutes a proof that the slowest case is xxx. Sure, it may be better to know why (especially when explaining it in editorials), but for the sake of posing it as a contest problem, I don't really see much of an issue with it, especially if the constraints are small enough that contestants can also stress-test it on their own computers.
I recall 735D - Taxes, the "Goldbach's conjecture problem", being controversial not because you had to assume Goldbach's conjecture, but because many people thought it was uninspired and was just a basic application of some well-known results, and a similar problem had appeared on Codeforces before.
If this conjecture is correct, there is no problem.
If it isn't correct(we get counter example), we can write research paper.
In any case, we are happy (⌒-⌒)
It is proven to be true for sufficiently small integers (4e18) which was enough here.
They are perfectly fine for 'Correctness', but have potential issue in other ways:
For the Goldbach's conjecture: people don't know it will have significant disadvantage. My first SRM problem MagicDiamonds (with change 'prime' to 'non-prime') requires this conjecture and was rejected by rng_58.
For the other case that proof is hard: people trying to proof their solution will have disadvantage. See this.
It's a good summary of common mistakes for non-experienced problemsetters, thanks for posting!
By the way, regarding the following statement:
Can you elaborate on the constant 4 here, please? I always used an empirical argument that using the two primes is almost the same as using one prime modulo of magnitude of their product (from which we immediately get the negligible probability of collision equal to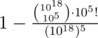
, but it is not really a strict proof.
I think it's just using a weaker result than the one normally assumed. The Schwartz-Zippel lemma applied to polynomial hashing states that the probability of collisions for two random strings of lengths m and n is max (m, n) / mod. The usual guess is that it's just 1 / mod. The post then states that the usual guess is hard to prove, and gives an example — rather familiar to you — when it's wrong.
So, the logic seems to be as follows: the usual guess is sometimes wrong, so unless we rigorously prove it's right, let's use a proven but weaker result. If that's indeed the author's intention, I see it as a step in wrong direction: the strings are usually non-random, so Schwartz-Zippel lemma does not apply. Indeed, for long enough Thue-Morse strings and hashing modulo a power of two, the collision will happen always, with probability 1, because there is no probabilistic selection of strings in the first place.
Ok, I got the concept.
By the way, why are you talking about non-random strings? In order to prove something we usually not depend on any probabilistic distribution on input strings, but we choose something (like the point we evaluate value of polynomials at) randomly from our side, and thus discard any possibility that somebody chooses an inappropriate string for us. That's why the Schwartz-Zippel lemma may be applied, and that's where the probability of success comes from. Strings should not be random in any sense.
The Thue-Morse string, for example, fails the hashes modulo 264 primarily because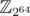
is not a field (in particular, there exists a polynomial of relatively small degree that has all odd residuals as roots).
You are right, the lemma needs the argument of the polynomial to be random, not the strings. Thank you for the correction!
OK then, I see a reason to use the weaker lemma instead of the stronger usual guess if the only solution the author's got is hashing, and proving the usual guess turns out to be hard. However, in practice, authors either rely on the usual guess (just calculating modulo different relatively prime values) or have a fast solution without hashing.
Rolling hash is (s0 + s1 x + s2 x2 + ...)%mod. Here mod = 109 + 7 is fixed and we choose x uniformly at random. When we compare two strings, if we do this for the same modulo but four distinct x 's, the probability of collision is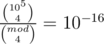
, and the probability that an unwanted collision happens in 
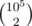pairs is at most 10 - 6.
Oh, I got it. I think the more popular way (at least in Russian-speaking community) is to use two different primes, not several hashes modulo single prime.
This might be a bit better because the empiric argument (that those two hash values are almost independent random variables) I given above somehow proves that two primes is enough for almost any problem.
Nice blog.
Also: stress testing your solution is very important but it doesn't mean you shouldn't prove the correctness. A perfect example is finding the two furthest points on the convex hull. There is a wrong solution that I couldn't fail with hours of stress testing.
I agree with your point, but sometimes it might be also an issue of your way of running stress tests. Particularly in the case of two furthest points on the convex hull and the common wrong solution using two pointers technique, the bad way to stress test would be to generate random polygons consisting of large number of points because they are pretty close to be regular and many wrong solutions may work for them.
I believe that if you stressed your solution on random polygons consisting of 3..6 points with coordinates in a small range (to force points get on a same line), you would almost immediately get the counter-test.
In the other words, making a good stress test also requires some experience from you.
I agree that quick stress testing on smart tests might be more valuable that hours of stress testing on random tests.
You are wrong about that furthest-points problem though. I was generating tests with small number of points but apparently the probability of getting the exact malicious test is extremely small, even if you choose the perfect N.
Can you elaborate on that wrong solution? I got curious.
I believe it's this one.
What's your viewpoint about searching problems which are solved by search algorithm such as alpha-beta pruning? Do you think this kind of problem should not appear in normal algorithm contest?
Yes. Such problems shouldn't appear unless we can prove that the intended solution is good.
An example of good searching problem is problem A of http://codeforces.me/gym/100110/attachments. Here we can simply try all tests.
A comment on 2. Time Complexity: GOOD: For this problem we can prove that the slowest case is xxx. Experimentally, my solution works for the input xxx under the given TL.
In practice, it is often difficult or virtually impossible to prove that a particular case is the true worst case because in a real computer we have complicated things that affect runtime.
For instance, denormal numbers are very slow and might create a "super-worst" case.
Memory caching mechanism might be an another example. Although I don't have a concrete example but I believe that for certain case it can greatly affect runtime. A similar thing is branch prediction.
Anyway, a writer should not set time limit too tight in my opinion.
On an irrelevant note, If I'm not mistaken rng_58 had a very "pleasant" experience with denormal numbers on World Finals :p.
Nice article, thanks!
Do you want to share other tips other than ways to make sure reference solution is good? (like: how to set Time Limit, how to make sure bad solutions can't pass, what things are good and what are bad?) I think that would be very helpful.
+1 for that, I'm particularly interested in how to make sure bad solutions can't pass without having to "guess" how it could be wrong. I'm used to spamming a lot (100000+) randomly generated small test cases but it have several too strong assumptions like "The solutions have to be fast enough on small test cases" etc.
What's your opinion of network flow problems? Since sometimes the constraints are rather large for O(V2E) flow algorithm. As contestants, we know that it's hard to approach this upper bound by random graphs. But as a problem setter, it's hard (at least for me) to prove that or construct worst case graph under certain problem background. For smaller constraints, the naive simplex method solution could be pretty fast.
Btw, thanks cgy4ever for many interesting flow problems on TopCoder :P
Hmm I didn't notice the issue about 'simplex method solution could be pretty fast': do you know some tasks that can be solved by simplex easily but will be harder for flow (of course I mean the problems with a flow solution as intended)?
I rarely use simplex so I don't know how to use it to solve problems (usually we need to prove that solutions will be integers, for simplex it may be hard).
Btw I encountered the reverse: this one was intended to be solved by simplex, but somehow everyone solved it by flow. :P
You can take literally almost every flow problem, LP formulation is almost always straightforward, whereas difficulty of flow network can significantly vary. A few examples of flow problems where I know there were some solutions using simplex: 1) D from last NEERC, 2) C from GCJ R2 2 years ago about some English and French words, 3) some SRM Hard problem by Lewin about lengthening edges in DAG so that all paths are as long as possible.
Surely, you can always create LP formulation from a flow network, however sometimes creating any LP formulation can be by far easier than one that corresponds to flow nrteork (what is the case in all mentioned problems).